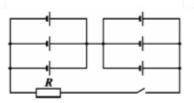
Пользуясь схемой, изображенной на рисунке, определить силу тока проходящего по резистору R = 23,6 Ом, если ЭДС и внутреннее сопротивление каждого элемента соответственно равны e=12 В и r=0,6 Ом. Сопротивление соединительных проводов ничтожно мало
Другие вопросы по теме Физика
Популярные вопросы
- заполнить сравнивать надо содержание .Как можно быстрее ,буду очень...
1 - √×√=36 решите пример или уравнение...
1 - ФІЗИКА У скільки разів абсолютне видовження мідного дроту більше, ніж...
1 - А) Где на момент избрания на царство находился сам Михаил Федорович...
2 - Запишите предложения, расставляя знаки препинания. Постройте схемы...
2 - ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА...
1 - Від чого залежить послідовність виконання операторів в формулах?...
1 - По теме Электрические явления...
1 - Классификацию инженерных сооружений их оборудование....
3 - 1.Какую из фотографий из вашего семейного альбома вы выбрали? 2.где...
2
1. Вычисление общего сопротивления цепи:
В данной схеме имеется два параллельно подключенных резистора (R и r), поэтому общее сопротивление можно вычислить по формуле:
1/Rt = 1/R + 1/r,
где Rt - общее сопротивление, R - значение сопротивления резистора R, r - значение сопротивления резистора r.
1/Rt = 1/23,6 + 1/0,6,
1/Rt = 0,04237 + 1,66667,
1/Rt = 1,70904.
Обращаем это число:
Rt = 1/1,70904,
Rt ≈ 0,5848 Ом.
2. Применение закона Ома:
Согласно закону Ома, сила тока (I) в цепи равна отношению напряжения (U) к сопротивлению (Rt):
I = U/Rt,
где U - ЭДС (электродвижущая сила).
Перейдем к числовым значениям:
I = 12/0,5848,
I ≈ 20,54 А.
Таким образом, сила тока, проходящего по резистору R, равна примерно 20,54 А.