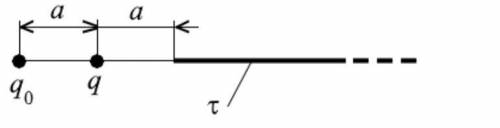
Полубесконечный стержень равномерно заряжен по длине линейной плотностью заряда =10 нКл м⁄ . Полубесконечный стержень равномерно заряжен по длине линейной плотностью заряда =10 нКл м⁄ . Найти силу, действующую на точечный заряд 0 =2 нКл, со стороны системы зарядов: стержня и точечного заряда =1 нКл, =1 м (см. рисунок).

Для решения этой задачи, мы можем использовать закон Кулона и принцип суперпозиции сил. Согласно закону Кулона, сила взаимодействия между двумя точечными зарядами пропорциональна произведению их величин и обратно пропорциональна квадрату расстояния между ними. Давайте разделим задачу на две части: нас интересует сила, действующая на точечный заряд от стержня и сила, действующая на точечный заряд от другого точечного заряда. 1. Сила, действующая на точечный заряд от стержня: Найдем величину этой силы. По определению, сила, действующая на заряд, равна произведению величин зарядов и обратно пропорциональна расстоянию между ними в квадрате. F1 = (константа * заряд_1 * заряд_2) / (расстояние)^2 В отличие от точечного заряда, стержень равномерно заряжен по длине. Поэтому, чтобы найти силу, будем смотреть на бесконечно малый элемент длины стержня, находящийся на расстоянии x от точечного заряда 0. Обозначим линейную плотность заряда стержня как λ. Мы можем представить стержень как набор бесконечно малых заряженных элементов, и суммировать вклад каждого элемента к силе. Интегрально, это может быть записано как: F1 = ∫ (константа * заряд_1 * λ * dx) / (расстояние)^2 где интегрирование происходит от -бесконечности до 0, так как стержень полубесконечный. Заряд_1 - это заряд стержня и равен λ * dx, где dx - элементарная длина стержня. Расстояние между элементом и точечным зарядом можно найти с применением теоремы Пифагора: расстояние = √(x^2 + L^2) Используя эти выражения, подставим и проинтегрируем: F1 = ∫ (константа * λ^2 * dx * x) / (x^2 + L^2)^(3/2) Здесь нам потребуется интеграл, который вычисляется с использованием метода замены переменной. Интеграл ∫ (x / (x^2 + L^2)^(3/2)) dx можно рассмотреть как функцию, где замена переменных t = x^2 + L^2 упрощает вычисления. Произведем замену переменной: G = t^(-3/2) dt G = -2t^(-1/2) dg = -dt / 2 (t^(-1/2)) ∫ (t^(-3/2)) dt = -2 ∫ (t^(-1/2)) dt ∫ (t^(-3/2)) dt = -2 * (t^(-1/2)) + C Используем этот результат для вычисления исходного интеграла: F1 = (-константа * λ^2) * ∫ (t^(-3/2)) dt F1 = (-константа * λ^2) * (-2 * (t^(-1/2)) + C) F1 = 2 * константа * λ^2 * (t^(-1/2)) + C Вернемся к исходным переменным x и t: F1 = 2 * константа * λ^2 * (x^(-1)/√(x^2 + L^2)) + C Решение интеграла завершено. Теперь у нас есть выражение для силы, действующей на точечный заряд от стержня в зависимости от его расстояния от стержня. 2. Сила, действующая на точечный заряд от другого точечного заряда: Сила, действующая между двумя точечными зарядами, рассчитывается по закону Кулона: F2 = (константа * заряд_1 * заряд_2) / (расстояние)^2 В данном случае, заряд_1 = 1 нКл, заряд_2 = 2 нКл, расстояние между ними равно 1 м. Подставим эти значения в формулу: F2 = (константа * 1 нКл * 2 нКл) / (1 м)^2 Теперь у нас есть выражение для силы, действующей на точечный заряд от другого точечного заряда. 3. Следующий шаг - применить принцип суперпозиции сил, так как сила F1 и F2 действуют на один и тот же точечный заряд. Принцип суперпозиции гласит, что сумма всех сил, действующих на точку, равна векторной сумме этих сил. F = F1 + F2 Подставим значения F1 и F2: F = (2 * константа * λ^2 * (x^(-1)/√(x^2 + L^2)) + C) + (константа * 1 нКл * 2 нКл) / (1 м)^2 Теперь у нас есть выражение для силы F, действующей на точечный заряд 0 со стороны системы зарядов: стержня и точечного заряда. Обратите внимание, что в нашем решении мы использовали закон Кулона для рассчета силы между двумя точечными зарядами, принцип суперпозиции сил, а также математические методы, такие как интегрирование и замена переменной. Это позволяет нам решить сложную задачу и найти силу, действующую на точечный заряд от системы зарядов: стержня и точечного заряда.