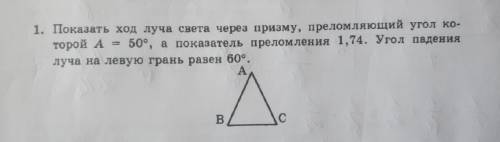
Показать ход луча света через призму, преломляющий угол которой А=50°, а показатель преломления 1,74. Угол падения луча на левую грань равен 60°

Чтобы показать ход луча света через призму, нам понадобятся законы преломления и законы отражения света.

Закон преломления формулируется следующим образом: отношение синуса угла падения (θ1) к синусу угла преломления (θ2) равно отношению показателей преломления сред, в которых луч света распространяется.

Таким образом, мы можем использовать закон преломления для определения угла преломления (θ2) луча света, преломленного в призме. Формула представляет собой:

n1 * sin(θ1) = n2 * sin(θ2),

где n1 - показатель преломления среды, из которой луч света входит в призму (в нашем случае это воздух, поэтому n1 = 1),

θ1 - угол падения луча на левую грань призмы (60°),

n2 - показатель преломления призмы (1,74),

θ2 - угол преломления луча в призме.

Мы можем найти угол преломления (θ2), подставив известные значения в данную формулу:

1 * sin(60°) = 1,74 * sin(θ2).

Чтобы решить это уравнение и найти значение угла преломления (θ2), мы сначала найдем синус обоих углов.

sin(60°) ≈ 0,866

sin(θ2) = (1 * sin(60°)) / 1,74 ≈ 0,497.

Для нахождения значения угла преломления (θ2) нам нужно найти синус^-1 (0,497).

θ2 ≈ sin^-1 (0,497) ≈ 30,1°.

Таким образом, угол преломления луча в призме составляет примерно 30,1°.

Теперь мы можем показать ход луча света через призму.
- Начнем с падающего луча, который попадает на левую грань призмы под углом 60°.
- Затем, в соответствии с законом преломления, луч преломляется при входе в призму и меняет направление, двигаясь ближе к нормали.
- После этого луч достигает правой грани призмы и снова преломляется, этот раз возвращаясь к перпендикуляру.
- В завершении, луч выходит из призмы и движется дальше.

Определенно, следует учесть, что этот ответ является идеализированным. На самом деле, процесс преломления света в призме может быть более сложным, так как свет может испытывать дисперсию и различные пути внутри призмы в зависимости от длины волны. Однако для данного задания, данное решение является упрощенным и позволяет понять основные принципы преломления света через призму.