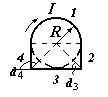
По плоскому контуру из тонкого провода течет ток I = 100 А. Определить магнитную индукцию В поля, создаваемого этим током в центре окружности (см. рис.). Радиус R изогнутой части контура равен 20 см.

Для определения магнитной индукции поля, создаваемого током в центре окружности, мы можем использовать формулу для расчета магнитной индукции на оси симметрии кругового контура:

B = (μ0 * I) / (2 * R)

где B - искомая магнитная индукция, μ0 - магнитная постоянная (приближенно равна 4π * 10^(-7) Тл/А·м), I - сила тока, R - радиус окружности.

Заменим известные значения в формуле:

B = (4π * 10^(-7) * 100) / (2 * 0.2)

B = 2π * 10^(-6) (Тл)

Таким образом, магнитная индукция поля, создаваемого током в центре окружности, равна 2π * 10^(-6) Тл.