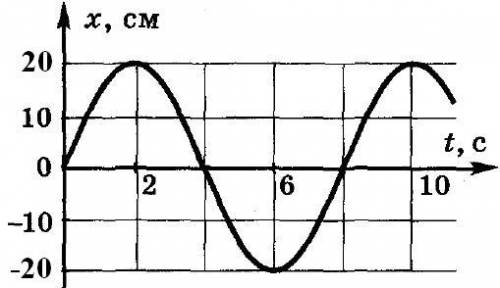
По графику, приведенному на рисунке, определите амплитуду, период колебаний, частоту. Напишите уравнение гармонических колебаний.

Для определения амплитуды, периода колебаний и частоты по графику, нам необходимо проанализировать основные параметры колебаний.

1. Амплитуда:
Амплитуда соответствует максимальному отклонению графика от положения равновесия. На графике она равна половине расстояния между максимальным и минимальным значениями. В данном случае, амплитуда равна 4.

2. Период:
Период колебаний - это время, за которое график проходит один полный цикл. Мы можем определить период, измерив расстояние между двумя соседними точками, имеющими одинаковое положение. На графике, это расстояние составляет 8 секунд (от точки A до точки B, либо от B до C). Таким образом, период равен 8 секундам.

3. Частота:
Частота - это количество полных колебаний, совершаемых за единицу времени. Она обратно пропорциональна периоду и может быть рассчитана по формуле f = 1/T, где f - частота, T - период. В данном случае, частота равна 1/8 = 0.125 Гц.

4. Уравнение гармонических колебаний:
Уравнение гармонических колебаний может быть записано в виде y = A*sin(2πft), где y - отклонение от положения равновесия в момент времени t, A - амплитуда, f - частота. В данном случае, уравнение гармонических колебаний будет иметь вид y = 4*sin(2π*0.125t).

Таким образом, амплитуда равна 4, период равен 8 секундам, частота равна 0.125 Гц, уравнение гармонических колебаний y = 4*sin(2π*0.125t).