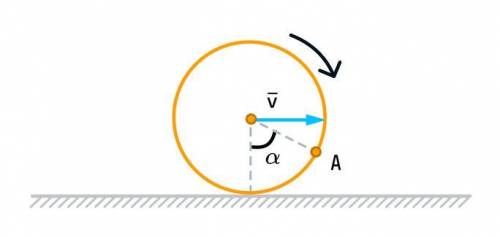
По горизонтальной поверхности без проскальзывания катится обруч радиусом R=0.5 со скоростью 2 м/с.Найдите скорость ∨А и ускорение αА точки А обруча относительно поверхности.Радиус, проведенный к точке А, образует угол α=60° с вертикалью

Чтобы ответить на данный вопрос, нам понадобятся знания о движении тела по окружности и о связи скорости и ускорения с радиусом обруча.

1. Начнем с определения скорости точки А обруча. Скорость - это векторная величина, которая показывает, как быстро меняется положение точки со временем. Для точки А она будет направлена по касательной к окружности в данной точке. Так как обруч катится без проскальзывания, скорость точки А равна скорости центра масс обруча. То есть, чтобы найти скорость точки А, нам нужно найти скорость центра масс обруча.

2. Для нахождения скорости центра масс обруча воспользуемся уравнением связи скорости, угловой скорости и радиуса. Угловая скорость (ω) равна скорости обруча (V) деленной на радиус обруча (R):
ω = V / R
Подставляем известные значения:
ω = 2 м/с / 0.5 м = 4 рад/с

3. Теперь мы знаем угловую скорость обруча. Чтобы найти скорость точки А, нужно найти проекцию скорости центра масс обруча на ось, проходящую через точку А. Радиус, проведенный к точке А, образует угол α=60° с вертикалью. Таким образом, нам понадобятся тригонометрические соотношения.
Проекция скорости точки А на ось, проходящую через точку А, обратно пропорциональна синусу угла α:
∨А = V * sin(α)
Подставляем известные значения:
∨А = 2 м/с * sin(60°) = 2 м/с * √(3) / 2 = √(3) м/с

4. Теперь перейдем к ускорению точки А обруча. Аналогично скорости, ускорение - это векторная величина, которая показывает, как быстро меняется скорость точки со временем. Ускорение точки А будет направлено вдоль касательной к окружности в данной точке. Чтобы найти ускорение точки А, нам понадобится радиус обруча и его угловое ускорение.

5. Угловое ускорение (α) определяется величиной углового ускорения и радиусом обруча. В данном случае угловое ускорение нам неизвестно, но мы можем найти его, используя второй закон Ньютона для вращательного движения:
α = a / R
где a - линейное ускорение (искомая величина)
Поскольку обруч катится без проскальзывания, линейное ускорение (a) равно ускорению свободного падения (g). То есть:
α = g / R
Подставляем известные значения:
α = 9.8 м/с^2 / 0.5 м = 19.6 м/с^2

6. Итак, мы нашли угловое ускорение обруча. Теперь нам осталось найти ускорение точки А, используя такую же тригонометрию, как и в пункте 3:
По аналогии с вектором скорости, проекция ускорения точки А обратно пропорциональна синусу угла α:
αА = α * sin(α)
Подставляем известные значения:
αА = 19.6 м/с^2 * sin(60°) = 19.6 м/с^2 * √(3) / 2 = 9.8 * √(3) м/с^2

Таким образом, скорость точки А обруча равна √(3) м/с, а ускорение точки А равно 9.8 * √(3) м/с^2.