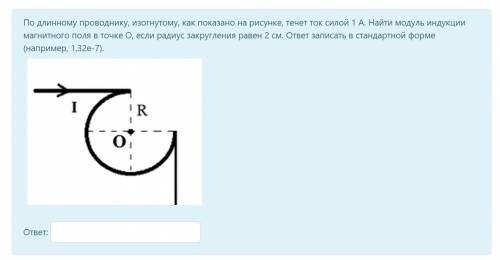
По длинному проводнику, изогнутому, как показано на рисунке, течет ток силой 1 А. Найти модуль индукции магнитного поля в точке О, если радиус закругления равен 2 см. ответ записать в стандартной форме (например, 1,32e-7).

Для решения данной задачи, нам понадобится использовать закон Био-Савара-Лапласа. Согласно этому закону, индукция магнитного поля в точке, создаваемого проводником с током, можно вычислить по формуле:

B = (μ₀ * I * dl * sinθ) / (4π * r²)

где:
B - индукция магнитного поля,
μ₀ - магнитная постоянная (равна 4πe-7 T*m/A),
I - сила тока,
dl - элементарный участок проводника,
θ - угол между элементарным участком проводника и радиусом закругления проводника,
r - расстояние от элементарного участка проводника до точки О.

В нашей задаче, мы имеем изогнутый проводник, состоящий из двух полуокружностей и отрезка. Для удобства решения, можно разбить проводник на несколько элементарных участков и вычислить индукцию магнитного поля в каждой из них. Затем, сложить полученные значения индукций магнитных полей для получения общего результата.

1. Рассмотрим первую полуокружность радиусом R₁ = 2 см. Для вычисления индукции магнитного поля в каждом элементарном участке нам потребуется угол дуги, по которой проходит данный участок. Учитывая, что угол на окружности равен π радиан (180 градусов), и что всего у нас есть полуокружность (180 градусов), получаем следующее:

угол дуги первой полуокружности = π

Теперь можем использовать формулу для вычисления индукции магнитного поля в каждом элементарном участке:

dB₁ = (μ₀ * I * dl₁ * sin(π)) / (4π * r₁²)
= (μ₀ * I * dl₁) / (4 * r₁²)
= (4πe-7 T*m/A * 1 A * dl₁) / (4 * (0.02 m)²)
= (πe-7 T*m) * dl₁ / (0.0008 m²)
= (3,14e-7) * dl₁ / (0,0008)

2. Рассмотрим отрезок проводника. Здесь угол дуги равен 0, так как это неокругленная часть проводника. Расстояние от этого участка до точки О будет составлять 2 см.

Теперь можем вычислить индукцию магнитного поля в этом участке:

dB₂ = (μ₀ * I * dl₂ * sin(0)) / (4π * r₂²)
= (μ₀ * I * dl₂) / (4 * r₂²)
= (4πe-7 T*m/A * 1 A * dl₂) / (4 * (0.02 m)²)
= (πe-7 T*m) * dl₂ / (0.0008 m²)
= (3,14e-7) * dl₂ / (0,0008)

3. Рассмотрим вторую полуокружность радиусом R₂ = 2 см. Как и в первом случае, угол дуги здесь равен π.

Вычислим индукцию магнитного поля в каждом элементарном участке:

dB₃ = (μ₀ * I * dl₃ * sin(π)) / (4π * r₃²)
= (μ₀ * I * dl₃) / (4 * r₃²)
= (4πe-7 T*m/A * 1 A * dl₃) / (4 * (0.02 m)²)
= (πe-7 T*m) * dl₃ / (0.0008 m²)
= (3,14e-7) * dl₃ / (0,0008)

4. Теперь необходимо сложить все индукции магнитных полей для получения общего результата:

B = dB₁ + dB₂ + dB₃ = (3,14e-7) * (dl₁ / 0,0008 + dl₂ / 0,0008 + dl₃ / 0,0008)

Ответ можно представить в стандартной форме, учитывая, что значение dl₁, dl₂ и dl₃ будет зависеть от размеров проводника и его геометрии. В данном случае, без конкретных числовых значений, невозможно точно определить модуль индукции магнитного поля в точке О.