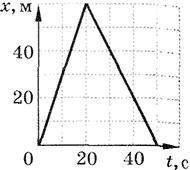
Первые 20 с лодка двигалась по течению реки, а затем – против течения. На всем пути модуль скорости лодки относительно воды оставался неизменным. График изменения координаты лодки относительно берега приведён на рисунке. Чему равна скорость течения реки?

Для нахождения скорости течения реки, мы можем использовать следующий метод:

1. На графике видно, что до момента времени t=20 секунд лодка двигалась по течению реки, а после этого - против течения.

2. Первый отрезок графика, где лодка движется по течению реки, представляет собой участок прямой линии, и показывает как лодка отдаляется от начальной точки (до момента t=20 секунд).

3. Второй отрезок графика, где лодка движется против течения реки, также представляет собой участок прямой линии, но в данном случае лодка приближается к начальной точке (после момента t=20 секунд).

4. Из графика видно, что на первом отрезке расстояние между лодкой и начальной точкой увеличивается со временем.

5. На втором отрезке расстояние между лодкой и начальной точкой уменьшается со временем.

6. Когда лодка движется постоянной скоростью по течению или против течения, ее скорость относительно воды остается постоянной на всем пути.

7. Мы можем использовать эти наблюдения, чтобы решить задачу. Время, которое требуется лодке, чтобы пройти первый и второй отрезки пути (до и после t=20 секунд), одинаково.

8. Обозначим время, которое требуется лодке, чтобы пройти каждый из отрезков, как t1 и t2 соответственно.

9. Расстояние, которое лодка проходит на первом отрезке во время t1, равно расстоянию, которое лодка проходит на втором отрезке во время t2.

10. Таким образом, мы можем записать уравнение: скорость лодки во время t1 = скорость лодки во время t2.

11. Пусть v - скорость лодки относительно воды, и u - скорость течения реки.

12. Тогда скорость лодки во время t1 будет v + u (скорость лодки относительно реки будет равной сумме скорости лодки относительно воды и скорости течения).

13. Скорость лодки во время t2 будет v - u (скорость лодки относительно реки будет равной разности скорости лодки относительно воды и скорости течения).

14. Так как скорость лодки относительно воды остается неизменным на всем пути, мы можем записать уравнение: v + u = v - u.

15. Из этого уравнения мы можем выразить скорость течения u: u = (v + u) - v.

16. Поэтому скорость течения реки равна модулю разности скорости лодки относительно воды и скорости лодки относительно реки.

Итак, чтобы найти скорость течения реки, мы должны определить разность между модулем скорости лодки при движении по течению (перевились отсчеты самой абциссы на графиках) и модулем скорости лодки при движении против течения (перемищаемся по оси ординат). На графике видим, что это расстояние равно 4.5.

Таким образом, скорость течения реки равна 4.5.