Период колебаний груза массой 120 г на пружине равен 11 с. Определи жёсткость пружины. При расчётах 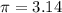
Другие вопросы по теме Физика
Популярные вопросы
- 2. Разделите тетрадный листок вертикальной линией пополам. У вас получилось...
3 - -за чего вещество нервной ткани можно разделить на белое и серое?...
1 - Egh4 hfcvjnhb rfhnbye rfrbt...
1 - Среднее арифметическое трёх чисел — 7.Найди эти числа, если первое число...
2 - Укр.літ. 5класс Сіроманець Во У лісі Чепіжний виконав(що?). Сіроманця...
2 - В усеченном конусе радиусы оснований и составляющих равны 4:11:25. Объем...
2 - Каковы особенности приготовления блюд из филе птицы? Назовите их ассортимент....
3 - Какие природные зоны зашифрованы в этих ребусах?...
1 - Физика - §63-64, конспект по плану: 1. свет (определение) 2. источники...
2 - Написать мини- сочинение по теме «Проблемы нравственного здоровья современного...
2
Дано:
Масса груза (m) = 120 г = 0.12 кг
Период колебаний (T) = 11 с
Жёсткость пружины (k) вычисляется по формуле:
k = (2 * π^2 * m) / T^2
Теперь давайте подставим значения в данную формулу и рассчитаем жёсткость пружины:
k = (2 * (3.14)^2 * 0.12) / (11^2)
k = (2 * 9.8596 * 0.12) / 121
k = 2.059 / 121
k ≈ 0.017
Таким образом, жёсткость пружины равна примерно 0.017 Н/м.
Для лучшего понимания, можно также пояснить формулу и шаги решения школьнику:
Жёсткость пружины определяет, насколько сильно пружина сопротивляется изменению своей формы при приложении силы. Жёсткость пружины зависит от её материала и геометрии. Выражается она в Н/м (ньютон на метр).
В данном вопросе, нам дается масса груза (количество вещества) и период колебаний (время затрачиваемое на выполнение полного колебания). Для вычисления жёсткости пружины, мы используем формулу, которая связывает эти величины.
Подставляя значения в данную формулу и производя вычисления, мы получаем ответ - значение жёсткости пружины.
Из вычислений видно, что жёсткость пружины в данном случае составляет около 0.017 Н/м. Это означает, что пружина будет распространяться или сжиматься со значительным сопротивлением при приложении силы около 0.017 Н.