1. Физика
  2. Пароход по реке преодолевает

Пароход по реке преодолевает расстояние между двумя за 6 ч, когда движется по течению, и за 8 ч - когда против течения. за какое время преодолеет расстояние между этими плот?

Alnaalnaalna Alnaalnaalna    1   15.06.2019 18:20    4

Ответы
Bairachock Bairachock  02.10.2020 02:14

Дано:

t_{1} = 6 ч

t_{2} = 8 ч

Найти: t-?

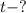
Решение. Легко убедится, что скорость плота совпадает со скоростью течения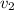 v_{2}. Согласно закону сложения скоростей составим еще два уравнения:

\left\{\begin{matrix} v_{2} = \dfrac{s}{t} \ \ \ \ \ \ \ \\ v_{1} + v_{2} = \dfrac{s}{t_{1}} \\ v_{1} - v_{2} = \dfrac{s}{t_{2}} \end{matrix}\right.

Вычтем от уравнения 2 уравнения 3, а первое домножим на 2:

\left \{ {\bigg{2v_{2} = \dfrac{2s}{t} \ \ \ \ \ \ } \atop \bigg{2v_{2} = \dfrac{s}{t_{1}} - \dfrac{s}{t_{2}} }} \right.

Получим:

\dfrac{2s}{t} = \dfrac{s}{t_{1}} - \dfrac{s}{t_{2}} }

\dfrac{2s}{t} = \dfrac{s}{t_{1}} - \dfrac{s}{t_{2}} }\\\\\dfrac{2s}{t} = \dfrac{s(t_{2} - t_{1})}{t_{1}t_{2}}}\\\\\dfrac{t}{2s} = \dfrac{t_{1}t_{2}}{s(t_{2} - t_{1})}\\\\t = \dfrac{2t_{1}t_{2}}{t_{2} - t_{1}}

Определим значение искомой величины:

t = \dfrac{2 \cdot 6\cdot 8}{8 - 6} = 48 ч

ответ: 48 ч

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
Sosushka Sosushka  08.02.2021 15:48
2. В сосуд высотой 60 см налиты ртуть и масло машинное Определите давление,которое оказывают жидкости на днососуда, если их объемы равны.​...
Марк2992 Марк2992  08.02.2021 15:48
Определите сопротивление каждого километра трамвайного медного провода, поперечное сечение которого равно 51 мм2...
ALIONA2020 ALIONA2020  10.04.2020 14:27
1. а)Чому волога яка міститься в грунті піднімається з нижніх шарів у верхні? б)Чому краплинки роси набувають кулястої форми?2. Якої деформації зазнає: а) опора моста?...
lololololo7 lololololo7  10.04.2020 14:28
скажите мне что такой МЕХАНИКА В АНАТОМИИ ЧЕЛОВЕКА...
kirill20060729 kirill20060729  10.04.2020 14:28
1. Как регистрируются частицы счетчиком Гейгера? чем заполнена трубка? 2. В чем особенность состояния паров жидкости в камере Вильсона? Что произойдет с траекторией...
artempirogov20p08sav artempirogov20p08sav  10.04.2020 14:28
Шанувальник фізики Отто фон Геріке на стіні одного із будинків встановив водяний барометр. Яка висота стовпчика води у трубці, якщо ртутний барометр цього дня показував...
саша4246 саша4246  10.04.2020 14:28
Визначити напругу нікелінового провідника довжиною 10 м, плошею перерізу 0,2 мм. Сила струму в провіднику 0,5 А.​...
ZnatokisRussia ZnatokisRussia  10.04.2020 14:28
1. Лампа даёт световой поток 750 лм. При этом поток илучення ранен 5,5 Вт. Если Излучение монохроматическое, чему равна его длина волны? 3. Газосветная лампа испускает...
ppoppo ppoppo  10.04.2020 14:28
Свинцовый кубик с длиной ребра 20 см поглотил 400 Дж радиоактивного излучения. Определите поглощенную дозу излучения. Плотность свинца 11300 кг/м3...
Alekskarpov Alekskarpov  12.11.2020 18:02
Какова масса бензина, расходуемого автомобилем, если расстояние между населенными пунктами Шахтерск-Донецк по трассе составляет 57 км, а расход топлива - 8 л на 100...

Популярные вопросы