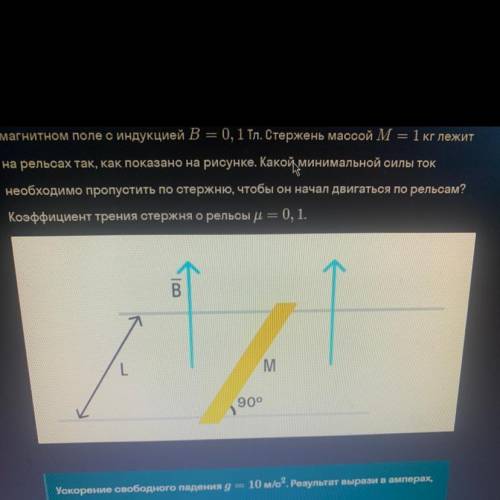
Параллельные рельсы, удалённые друг от друга на расстояние L = 0, 5 м, находятся на горизонтальной плоскости в однородном вертикальном
магнитном поле с индукцией B = 0,1 Tл. Стержень массой M = 1 кг лежит
на рельсах так, как показано на рисунке. Какой минимальной силы ток
необходимо пропустить по стержню, чтобы он начал двигаться по рельсам?
Коэффициент трения стержня о рельсы u= 0,1.
G=10

Для того чтобы решить эту задачу, нам необходимо использовать закон электродинамической индукции Фарадея и силы трения.

Первым шагом нужно найти силу трения, которая препятствует движению стержня по рельсам. Формула для расчета силы трения выглядит следующим образом:

Fтр = u * N,

где Fтр - сила трения, u - коэффициент трения, N - нормальная сила.

Нормальная сила N определяется как проекция силы тяжести стержня на нормаль к поверхности. В данном случае, так как стержень лежит на рельсах, нормальная сила будет равна N = M * g * cos(θ), где M - масса стержня, g - ускорение свободного падения, θ - угол наклона рельсов к горизонту. В данном случае рельсы горизонтальны, поэтому θ = 0 и cos(θ) = 1, следовательно, N будет равно N = M * g.

Теперь, когда мы знаем нормальную силу, можем вычислить силу трения:

Fтр = u * N = u * M * g.

Вторым шагом решения является применение закона электродинамической индукции Фарадея. Согласно этому закону, электрическая сила, действующая на проводник, пропорциональна скорости, с которой проводник движется в магнитном поле и величине магнитного поля:

Fэл = B * v * l,

где Fэл - электрическая сила, B - индукция магнитного поля, v - скорость проводника, l - длина предполагаемого участка проводника, на котором магнитное поле действует.

В нашем случае, участок проводника, на котором действует магнитное поле, равен l = L (расстояние между рельсами), и так как стержень начинает двигаться только после достижения критической скорости, скорость v равна 0.

Теперь мы можем записать второй закон Ньютона:

∑F = Fтр - Fэл.

Поскольку стержень двигается свободно без внешней силы, ∑F равно нулю, и мы имеем:

0 = Fтр - Fэл.

Заменим выражения для силы трения и электрической силы:

0 = u * M * g - B * v * L.

Для того чтобы найти критическую скорость, при которой стержень начинает двигаться, мы должны приравнять выражение к нулю:

0 = u * M * g - B * v * L.

Теперь будем решать уравнение относительно v:

B * v * L = u * M * g.

v * L = u * M * g / B.

v = u * M * g / (B * L).

Подставив значения, получим результат:

v = (0,1 * 1 * 10) / (0,1 * 0,5) = 2 м/c.

То есть, критическая скорость проводника, при которой стержень начинает двигаться по рельсам, равна 2 м/c.

Наконец, чтобы найти минимальную силу тока, необходимую для достижения критической скорости, мы можем использовать формулу:

Fэл = B * I * l,

где Fэл - электрическая сила, I - сила тока.

Обратимся к закону электродинамической индукции Фарадея и подставим значения:

B * v * l = B * I * l.

I = v.

I = 2 А.

Таким образом, минимальная сила тока, необходимая для начала движения стержня по рельсам, равна 2 А.