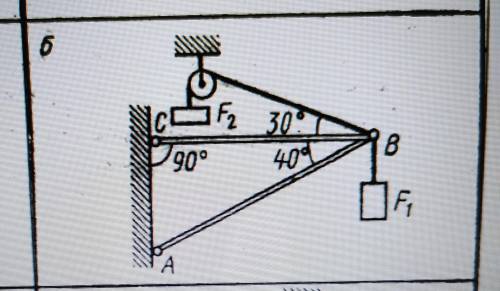
Определите реакции стержней , удерживающих грузы 0,3 и 0,8. массой стержня пренебречь .

Для определения реакций стержней, удерживающих грузы 0,3 и 0,8, мы можем использовать условия равновесия. Условие равновесия гласит, что сумма сил должна быть равна нулю, а сумма моментов должна быть равна нулю.

Для начала, давайте обозначим неизвестные нам реакции стержней как R1 и R2. Затем, распишем силы, действующие на каждый груз:

На груз массой 0,3:
- Вес груза, направленный вниз и равный массе груза умноженной на ускорение свободного падения g. Обозначим эту силу W1.
- Реакция R1, направленная вверх. Обозначим эту силу R1.

На груз массой 0,8:
- Вес груза, направленный вниз и равный массе груза умноженной на ускорение свободного падения g. Обозначим эту силу W2.
- Реакция R2, направленная вверх. Обозначим эту силу R2.

Исходя из условия равновесия:

Сумма сил в вертикальном направлении должна быть равна нулю:
R1 + R2 - W1 - W2 = 0 .....(1)

Сумма моментов должна быть равна нулю. Выберем силовой момент напротив точки O (начало оси координат) для удобства.
Против часовой стрелки будут положительные значения моментов.

Момент груза массой 0,3 относительно точки O:
- Расстояние от точки O до груза массой 0,3 умноженное на силу R1, равно длине стержня L1.
Момент = L1 * R1

Момент груза массой 0,8 относительно точки O:
- Расстояние от точки O до груза массой 0,8 умноженное на силу R2, равно длине стержня L2.
Момент = L2 * R2

Сумма моментов остальных сил должна быть равна нулю:
L1 * R1 - L2 * R2 = 0 .....(2)

Решая систему уравнений (1) и (2), мы сможем определить значения R1 и R2.

Для упрощения решения, мы можем использовать численные значения, предоставленные на изображении. По изображению, расстояние L1 равно 2 м, а расстояние L2 равно 4 м.

Подставим численные значения и решим систему уравнений:

R1 + R2 - 0,3g - 0,8g = 0 .....(1)
2R1 - 4R2 = 0 .....(2)

4R1 + 4R2 - 0,3g - 0,8g = 0 (уравнение (1) умножено на 2)
2R1 - 4R2 = 0

6R1 - 0,8g = 0
2R1 = 4R2

Из второго уравнения: R1 = 2R2

6(2R2) - 0,8g = 0 (подставляем R1 во второе уравнение)
12R2 - 0,8g = 0

12R2 = 0,8g
R2 = 0,8g / 12
R2 = 0,0667g

R1 = 2R2
R1 = 2 * 0,0667g
R1 = 0,1333g

Таким образом, реакция стержня, удерживающего груз массой 0,3, равна 0,1333g, а реакция стержня, удерживающего груз массой 0,8, равна 0,0667g.