определите полную механическую энергию колебаний грузика на пружине и наибольшую скорость его движений если масса груза 100 грамм жесткость пружины 0,5 кН/м амплитуда колебаний 20 см

Ответы

мага7626 07.04.2021 12:57

Дано:

m = 100 гр = 0,1 кг

k = 0,5 кН/м = 500 Н/м

A = 20 см = 0,2 м

-------------------------------------

Найти:

E - ? υ(max) - ?

Запишем формулы кинетической энергий и потенциальной энергий тела при деформированной пружины:

$Ekin = \frac{mv^{2}}{2}$ - Кинетическая энергия

$Epon = \frac{kx^{2}}{2}$ - Потенциальная энергия

Теперь мы используем закон сохранения механической энергий:

$E = Ekin + Epon = \frac{mv^{2}}{2}+\frac{kx^{2}}{2}=const$ - Закон сохранение энергий

Максимальное отклонение равно амплитуде колебания, скорость в этом энергий равно нулю, давайте запишем:

Пусть υ = 0, тогда: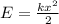 $E = \frac{kx^{2}}{2}$

Пусть x = A, следовательно: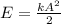 $E = \frac{kA^{2}}{2}$ - Общая формула сохранения механической энергий.

E = 500 Н/м × (0,2 м)²/2 = 500 Н/м × 0,04 м²/2 = 20 Н×м/2 = 10 Н×м = 10 Дж

Максимальная скорость достигается в положений равновесия, при этом его отклонение равно нулю:

Пусть x = 0, тогда: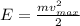 $E = \frac{mv^{2}_{max} }{2}$ , следовательно мы получим:

$v^{2}_{max}=\frac{2E}{m} \Rightarrow v_{max}=\sqrt{\frac{2E}{m}} \Rightarrow v_{max}=\sqrt{\frac{2*\frac{kA^{2}}{2}}{m}} \Rightarrow v_{max}=\sqrt{\frac{kA^{2}}{m}} \Rightarrow v_{max}=A\sqrt{\frac{k}{m}}$

υ(max) = 0,2 м × √500 Н/м/0,1 кг = 0,2 м × √500 кг×м/с²/м / 0,1 кг = 0,2 м × √500 кг/с²/0,1 кг = 0,2 м × √5000 1/с² = 0,2 м × √5000 с⁻² ≈ 0,2 м × 70,71 с⁻¹ ≈ 14,142 м/с ≈ 14,14 м/с

ответ: E = 10 Дж, υ(max) = 14,14 м/с

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Физика