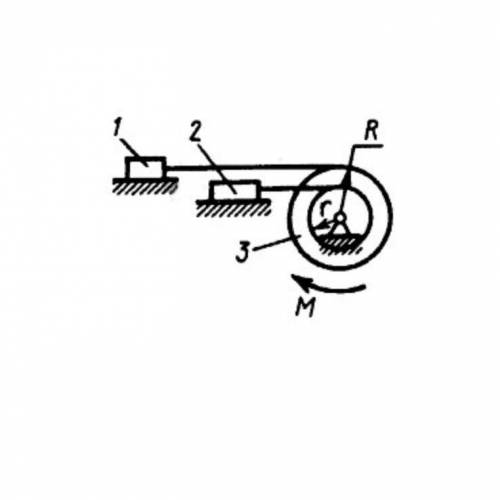
Определить угловое ускорение барабана если его момент инерции относительно оси вращения I3 = 0,1 кг • м , момент пары сил, действующей на барабан, М = 0,6 Н • м, массы тел m1 = m2 = 10 кг, радиусы R = 0,2 м, r = 0,1 м.
Другие вопросы по теме Физика
Популярные вопросы
- Выписать современные методы регулирования труда наемных работников...
3 - Из окошка высадился стол .и пошёл , пошёл пошёл пошёл. какие опасности письма...
1 - Покрылся,наполнился,сверкала,сияло,прогрело,тянулись,расцвели. какого время...
1 - Вназвании какого города глухих звуков больше , чем звонких?...
3 - Ввазе лежали яблоки и груши петя взял из вазы 6 яблок и 6 груш при этом...
3 - Как сделать jim likes to play with friends...
3 - 1)семейства крестоцветные / мотыльковые / розоцветные / сложноцветные /...
1 - Пройдя 6 часть пути, путник понял, что ему осталось пройти 15 км. каков...
2 - Дерево не большой высоты, листья видоизменены и напоминают чешуйки, ветви...
3 - Выделить корень в словах: берётся,даётся,отложил,бросил,стелет,спать,вырастишь,сдерёт,положил,задирает,гуляет,запирает,потчует...
3
Шаг 1: Определение суммарного момента сил, действующих на барабан.
Изображенный на картинке барабан находится под действием двух сил - пары грузов и натяжения нити. Натяжение нити направлено к центру барабана, поэтому его момент равен нулю. Таким образом, суммарный момент сил, действующих на барабан, равен только моменту пары сил, обозначенному М.
Шаг 2: Определение момента инерции барабана относительно его оси вращения.
Момент инерции барабана относительно его оси вращения обозначен I3 и равен 0,1 кг • м.
Шаг 3: Применение второго закона Ньютона для вращательного движения.
Второй закон Ньютона для вращательного движения гласит, что суммарный момент сил, действующих на тело, равен произведению углового ускорения на его момент инерции:
ΣM = Iα,
где ΣM - суммарный момент сил, I - момент инерции, α - угловое ускорение.
Шаг 4: Расчет углового ускорения.
Из предыдущих шагов, мы знаем, что ΣМ равен М, а I равно 0,1 кг • м. Подставим эти значения в уравнение:
М = Iα.
А теперь найдем угловое ускорение, разделив обе части уравнения на I:
α = М / I.
Подставим значения: М = 0,6 Н • м, I = 0,1 кг • м:
α = 0,6 Н • м / 0,1 кг • м = 6 рад/с².
Ответ: Угловое ускорение барабана равно 6 рад/с².