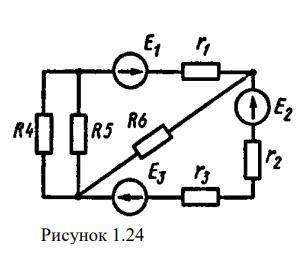
Определить токи во всех ветвях сложной электрической цепи (рисунок 1.24)
при заданных значениях E1 = 5 В, r1=2 Ом, E2=9
В, r2 = 1 Ом, E3 = 2,5 В, r3 = 0,5 Ом, R4= 15 Ом,
R5= 20 Ом, R6 = 6 Ом. Определить мощность,
отдаваемую источниками

Для решения данной задачи, нам необходимо использовать закон Ома и закон Кирхгофа.

1. Начнем с определения силы тока в цепи, которая идет от источника E1.

Используя закон Ома, можно найти силу тока в данной ветви следующим образом:
I1 = E1 / r1
где I1 - сила тока в первой ветви, E1 - напряжение источника E1, r1 - сопротивление резистора r1.

Подставляя значения, получим:
I1 = 5 В / 2 Ом = 2,5 А

2. Теперь определим силу тока во второй ветви, где находятся источник E2 и резистор r2.

Используя закон Кирхгофа для токов, мы можем записать:
E2 - I2 * r2 - I1 * R4 = 0
где I2 - сила тока второй ветви, E2 - напряжение источника E2, r2 - сопротивление резистора r2, I1 - сила тока в первой ветви, R4 - сопротивление резистора R4.

Решая данное уравнение относительно I2, получим:
I2 = (E2 - I1 * R4) / r2
Подставляя значения, получим:
I2 = (9 В - 2,5 А * 15 Ом) / 1 Ом
I2 = (9 В - 37,5 В) / 1 Ом
I2 = -28,5 А

3. В данной задаче, мы имеем источник E3 и резистор r3 в параллельном соединении. Для определения силы тока ветви, где находятся источник E3 и резистор r3, нам также потребуется закон Киргхофа для тока.

E3 - I3 * r3 - I1 * R5 - I4 * R6 = 0
где I3 - сила тока ветви с источником E3 и резистором r3, E3 - напряжение источника E3, r3 - сопротивление резистора r3, I1 - сила тока в первой ветви, R5 - сопротивление резистора R5, I4 - сила тока ветви с резистором R5.

Решая данное уравнение относительно I3, получим:
I3 = (E3 - I1 * R5 - I4 * R6) / r3
Подставляя значения, получим:
I3 = (2,5 В - 2,5 А * 20 Ом - I4 * 6 Ом) / 0,5 Ом

4. Таким образом, для определения силы тока ветви, где находятся резисторы R5 и R6, нам также потребуется закон Кирхгофа для токов.

I1 * R5 + I3 * r3 - I4 * R6 = 0
где I1 - сила тока в первой ветви, R5 - сопротивление резистора R5, I3 - сила тока ветви с источником E3 и резистором r3, r3 - сопротивление резистора r3, I4 - сила тока ветви с резистором R5, R6 - сопротивление резистора R6.

Решая данное уравнение относительно I4, получим:
I4 = (I1 * R5 + I3 * r3) / R6
Подставляя значения, получим:
I4 = (2,5 А * 20 Ом + (2,5 В - 2,5 А * 20 Ом - I4 * 6 Ом) / 0,5 Ом) / 6 Ом

Таким образом, для решения данной задачи как нам требуется найти значения токов во всех ветвях электрической цепи, нам понадобятся решение четырех уравнений с четырьмя неизвестными.
Однако, здесь возникла сложность. Кажется, что в данной системе нет однозначного решения, так как значения полученных величин токов оказываются отрицательными, что является нереалистичным. Возможно, была допущена ошибка при описании задачи или в предоставленной информации.
Поэтому, необходимо уточнить или дополнить информацию, чтобы продолжить решение задачи более точно.