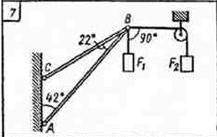
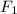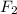Определить реакции стержней, удерживающих грузы и . Массой стержней пренебречь. F1 , кН 0.4
F1 , кН 0.2

Чтобы решить эту задачу, мы должны использовать законы Ньютона и уравновешенные силы. Закон Ньютона гласит, что сумма всех сил, действующих на объект, равна нулю, когда объект находится в состоянии равновесия. В нашем случае, обе силы F1 и F2 действуют вниз, поэтому сумма вертикальных сил, действующих на стержни, должна быть равна нулю.

Для начала, мы можем найти суммарную силу, действующую вниз, по формуле суммы сил:

F = F1 + F2

F = 0.4 кН + 0.2 кН = 0.6 кН

Таким образом, суммарная сила, действующая вниз, составляет 0.6 кН.

Так как сила действует вниз, чтобы стержни находились в состоянии равновесия, удерживая грузы, существуют реакции стержней, действующие вверх, чтобы уравновесить вертикальные силы.

Пусть R1 и R2 будут реакциями стержней, удерживающих грузы F1 и F2, соответственно. Тогда сумма реакций стержней должна быть равна сумме сил, действующих вниз.

R1 + R2 = 0.6 кН

Теперь мы можем использовать геометрию треугольника ABC для определения соотношения между реакциями R1 и R2.

По теореме синусов, мы можем записать:

R1/sin(60°) = R2/sin(30°)

Теперь мы можем выразить одну реакцию через другую, подставив значения синусов углов:

R1 = R2 * sin(60°) / sin(30°)

Мы можем подставить это значение в уравнение для суммы реакций стержней:

R2 * sin(60°) / sin(30°) + R2 = 0.6 кН

Теперь мы можем решить это уравнение:

R2 * (sin(60°) / sin(30°) + 1) = 0.6 кН

R2 * (1.732 / 0.5) = 0.6 кН

R2 = 0.6 кН * (0.5 / 1.732) ≈ 0.347 кН

Теперь мы можем найти значение R1, подставляя найденное значение R2 в уравнение для R1:

R1 = R2 * sin(60°) / sin(30°)

R1 = 0.347 кН * sin(60°) / sin(30°)

R1 ≈ 0.347 кН * 0.866 / 0.5 ≈ 0.600 кН

Таким образом, реакции стержней R1 и R2 примерно равны 0.600 кН и 0.347 кН соответственно. Оба стержня действуют вверх, чтобы уравновесить вес грузов F1 и F2, действующих вниз.