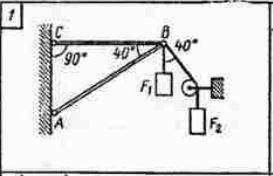
Определить реакции стержней, удерживающих грузы F1 и F2. Массой стержней пренебречь. F1=0,4 кН, F2=0,5 кН.

Для определения реакций стержней, удерживающих грузы F1 и F2, можно воспользоваться принципом равновесия. Согласно этому принципу, если тело находится в состоянии равновесия, то сумма всех действующих на него сил и моментов должна равняться нулю.

В данном случае, у нас имеются две силы F1 и F2, действующие на стержни, а также реакции стержней R1 и R2. Обозначим расстояние между точкой приложения силы F1 и опорой стержня как d1, а расстояние между точкой приложения силы F2 и опорой стержня как d2.

Для начала рассмотрим равновесие по вертикали. Согласно принципу равновесия, сумма вертикальных сил должна быть равна нулю. Так как на стержень не действуют вертикальные силы, то реакции стержней R1 и R2 будут равны по модулю и противоположны по направлению, чтобы компенсировать действие грузов F1 и F2. Обозначим модуль реакции стержня как R.

Теперь рассмотрим равновесие по горизонтали. Сумма горизонтальных сил также должна быть равна нулю. Семейство реакций стержней R1 и R2 не создает горизонтальных сил. Груз F1 создает горизонтальную силу F1x, а груз F2 - горизонтальную силу F2x. Так как сумма горизонтальных сил должна быть равна нулю, то F1x и F2x должны компенсироваться. Груз F1 находится на расстоянии d1 от опоры стержня, поэтому F1x = F1 * d1 / L, где L - длина стержня. Аналогично, F2x = F2 * d2 / L.

Таким образом, для определения реакций стержней R1 и R2, необходимо следовать следующим шагам:

1. Определить горизонтальные силы F1x и F2x, используя формулы F1x = F1 * d1 / L и F2x = F2 * d2 / L.
2. Равновесие по вертикали гарантирует, что R1 = R2 = R.
3. Сумма вертикальных сил также должна быть равна нулю. Следовательно, R1 + R2 = F1 + F2.
4. Подставить значения F1, F2, d1, d2 и L в уравнение суммы вертикальных сил и решить его относительно R1 и R2.
5. Рассчитать F1x и F2x, используя значения R1, R2, d1, d2 и L, а также формулы F1x = F1 * d1 / L и F2x = F2 * d2 / L.
6. Ответ представить в виде: R1 = ..., R2 = ..., F1x = ..., F2x = ..., где вместо многоточий будут указаны конкретные числовые значения реакций стержней и горизонтальных сил.