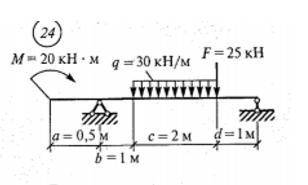
Определить опорные реакции балки на двух опорах по данным

Для определения опорных реакций балки на двух опорах, нам необходимо использовать условие равновесия. Перед тем, как мы начнем, давайте разберемся с терминологией.

Опора - это место, где балка поддерживается и может двигаться в определенных направлениях.
Опора может быть заделанной (фиксированной) или шарнирной (свободной).
Опорные реакции - это силы или моменты, с которыми опора действует на балку.

В данном случае, у нас имеется балка с двумя опорами. По условию, на балке распределено равномерно распределенное нагрузочное воздействие, величину которого требуется определить.

Для начала, обозначим реакции опоры: сила и момент считаются положительными, если они действуют вправо или по часовой стрелке, соответственно.

Используя условие равновесия, можем записать уравнения положения для опорных реакций:

∑F_x = 0 -> R_A - F = 0 (уравнение для горизонтальных сил)
∑M_A = 0 -> R_B * L - F * (L/2) - M = 0 (уравнение для моментов относительно точки A, где L - длина балки)

Теперь давайте разберемся, что означают эти уравнения.

В первом уравнении ∑F_x = 0, сумма горизонтальных сил в системе равна нулю. Здесь R_A - сила реакции опоры A, F - сила равномерно распределенного нагрузочного воздействия. Так как сумма горизонтальных сил равна нулю, то реакция опоры A равна силе нагрузки.

Во втором уравнении ∑M_A = 0, сумма моментов относительно точки A равна нулю. Здесь R_B - сила реакции опоры B, L - длина балки, F - сила нагрузки (равномерно распределенное нагрузочное воздействие), M - момент (перпендикулярная сила, действующая на балку).

Теперь, подставим получившиеся уравнения в формулы и решим их.

Из первого уравнения имеем:
R_A - F = 0
R_A = F

Из второго уравнения получаем:
R_B * L - F * (L/2) - M = 0

Теперь определим момент M. Зная силу нагрузки F и длину балки L, мы можем выразить момент следующим образом:
M = F * (L/2)

Подставим полученное выражение для момента во второе уравнение:
R_B * L - F * (L/2) - F * (L/2) = 0

Упростим уравнение:
R_B * L - F * L = 0

Разделим оба члена равенства на L:
R_B - F = 0
R_B = F

Таким образом, опорные реакции балки на двух опорах будут следующими:
R_A = F
R_B = F

Ответ: Реакция опоры A будет равна силе нагрузки F, а реакция опоры B тоже будет равна силе нагрузки F.