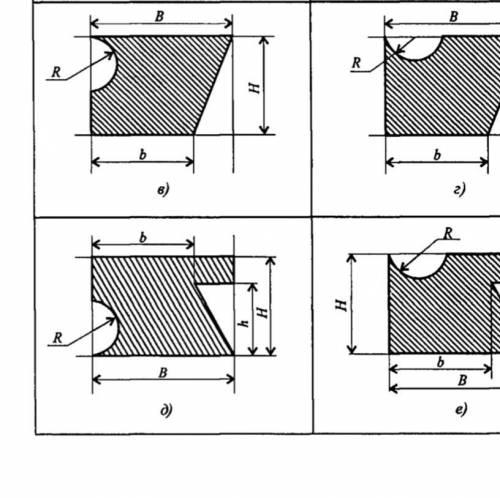
Определить координаты центра тяжести заданного сечения. Рисунок: «Д». B, мм=160. b, мм=120. H, мм=140. h, мм=110. R, мм=40.

Для определения координат центра тяжести заданного сечения, нужно разделить его на несколько простых геометрических фигур, для каждой из которых мы можем определить координаты центра тяжести. После этого мы сможем рассчитать общий центр тяжести с помощью формулы суммы моментов.

На данном рисунке мы имеем сечение, состоящее из прямоугольника с габаритами B и H, треугольника с основанием b и высотой h, и полукруга радиусом R.

Для начала, рассмотрим прямоугольник. Центр прямоугольника будет находиться в его геометрическом центре, поэтому его координаты будут:
Xc = B/2
Yc = H/2

Теперь рассмотрим треугольник. Чтобы найти его центр тяжести, можно использовать формулу для координат центра масс треугольника:
Xc = (2b + b) / 3
Yc = (h + h + H) / 3

Наконец, рассмотрим полукруг. Для полукруга мы можем использовать формулу для координат его центра масс:
Xc = R
Yc = R + (H - 2R)/2 = R + H/2 - R = H/2 + R

Теперь, чтобы найти общие координаты центра тяжести, мы можем использовать формулу суммы моментов:
Xсобщ = (Xc1 * S1 + Xc2 * S2 + Xc3 * S3) / (S1 + S2 + S3)
Yсобщ = (Yc1 * S1 + Yc2 * S2 + Yc3 * S3) / (S1 + S2 + S3)

Где Xc1, Xc2, Xc3 и Yc1, Yc2, Yc3 - координаты центров тяжести каждой фигуры, S1, S2, S3 - площади этих фигур.

Подставляя известные значения, получим:
Xсобщ = (B/2 * BH + (2b + b)/3 * (bh/2) + R * (πR^2)/2) / (BH + (bh/2) + (πR^2)/2)
Yсобщ = (H/2 * BH + (h + h + H)/3 * (bh/2) + (H/2 + R) * (πR^2)/2) / (BH + (bh/2) + (πR^2)/2)

Остается только подставить известные значения (B = 160, b = 120, H = 140, h = 110, R = 40) и произвести расчеты:

Xсобщ = (160/2 * 160*140 + (2*120 + 120)/3 * (120*110/2) + 40 * (π40^2)/2) / (160*140 + (120*110/2) + (π40^2)/2)
Yсобщ = (140/2 * 160*140 + (110 + 110 + 140)/3 * (120*110/2) + (140/2 + 40) * (π40^2)/2) / (160*140 + (120*110/2) + (π40^2)/2)

Подставляя значения в калькулятор, можно получить ответ:
Xсобщ ≈ 109.79 мм
Yсобщ ≈ 97.83 мм

Таким образом, центр тяжести заданного сечения имеет координаты примерно X = 109.79 мм, Y = 97.83 мм.