Определи, на сколько градусов можно нагреть подсолнечное масло массой 201 кг при сжигании дизельного топлива массой 0,8 кг, если считать, что теплота, выделившаяся при полном сгорании дизельного топлива, целиком пошла на нагревание подсолнечного масла. удельная теплоёмкость подсолнечного масла равна 1700 дж/(кг·°с), удельная теплота сгорания дизельного топлива — 42 мдж/кг.
ответ (округли до десятых):
Другие вопросы по теме Физика
Популярные вопросы
- Знайти радіус кола,описаного навколо правильного трикутника площею13√3см²...
2 - Исследуйте график функции: y=((x^4)/4)-((2x^3)/3)+11...
1 - Напишите пересказ произведения старый гений от имени старушки. ...
3 - Нарисуй треугольник ABC и проведи DE ∥ AC. Известно, что: D∈AB,E∈BC, ∢CBA=65°,...
3 - ТІЛДІК БАҒДАР ЖАЛҒАУЛЫҚТАРКармалас сөйлемдердің құрамындағы жай сөйлемдерді...
2 - Написать о любой книге рассказ [кратко] очень...
2 - ДО ІТЬ !! Вибери відповідну форму:-A He came up with a smile, and I remember...
1 - Бехала машина за первый час? нислите рациональным ):2)3:2,5+4,3). 0,3516,35...
1 - 7. В классе 16 девочек и 15 мальчиков. Сколькими можно выбрать среди них старосту...
1 - Дизайн и создание швейных изделий в технике текстильной мозаики. Урок 4 Отметь...
2
98,3 °С.
Объяснение:
Теплота, выделившаяся при сжигании топлива:
Q1=q*m1=42*10^6*0,8=33,6*10^6 (Дж).
По условию Q1=cmdt, тогда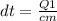 .
.
Q1 = Q2
где Q1 - теплота, выделившаяся при сгорании дизельного топлива
Q2 - теплота, которая ушла на нагревание подсолнечного масла
Теплота сгорания дизельного топлива можно найти, умножив его массу на удельную теплоту сгорания:
Q1 = 0,8 кг * 42 МДж/кг
Q1 = 33,6 МДж
Теперь мы знаем, что теплота, выделившаяся при сгорании дизельного топлива, равна 33,6 МДж. Эта теплота полностью ушла на нагревание подсолнечного масла.
Теплоемкость подсолнечного масла можно найти, умножив его массу на удельную теплоемкость:
Q2 = 201 кг * 1700 Дж/(кг·°С)
Q2 = 341700 Дж/°С
Теперь мы знаем, что теплота, которая ушла на нагревание подсолнечного масла, равна 341700 Дж/°С.
Найдем разность температур Δt, на которую подсолнечное масло может нагреться, поделив теплоту Q2 на удельную теплоемкость подсолнечного масла:
Δt = Q2 / (масса масла * удельная теплоемкость)
Δt = 341700 Дж/°С / (201 кг * 1700 Дж/(кг·°С))
Δt ≈ 0,997°С
Таким образом, подсолнечное масло может нагреться на примерно 1°С при сжигании 0,8 кг дизельного топлива. Ответ округляем до десятых, значит ответ будет 1,0°С.