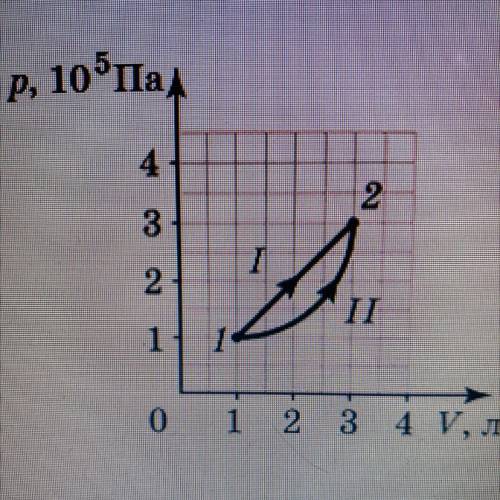
Определи изменение внутренней энергии при переходе газа из состояния 1 в состояние 2 при процессах I и II.

800 дж

Для определения изменения внутренней энергии при переходе газа из состояния 1 в состояние 2 при процессах I и II, мы можем использовать первый закон термодинамики, также известный как закон сохранения энергии.

Закон сохранения энергии гласит, что изменение внутренней энергии (ΔU) равно сумме работы (W), произведенной над системой, и тепла (Q), переданного системе:

ΔU = Q + W

Процессы I и II показаны на диаграмме pV (давление-объем) газа. Для определения работы, сначала нам нужно определить площадь под кривой процесса для каждого случая.

Процесс I:
- Начинаем в состоянии 1, где объем равен V1 и давление равно p1.
- Затем переходим в состояние 2, где объем равен V2 и давление равно p2.
- В этом процессе кривая является гиперболой и неоднородной.

Чтобы определить площадь под кривой процесса I, мы можем разбить ее на маленькие прямоугольники и сложить их площади:

W1 = ∫ p dV

Так как кривая неоднородна, нам нужно взять интеграл по кривой. Для упрощения расчетов, мы можем разбить кривую на несколько частей, где каждая часть представляет собой прямоугольник и известен объем и давление.

Определение тепла (Q1) в процессе I должно быть дано в условии задачи. Предположим, что нам дано, что процесс I является адиабатическим (Q1 = 0), то есть никакое тепло не переходит между системой и окружающей средой.

Таким образом, изменение внутренней энергии (ΔU1) в процессе I будет равно сумме работы (W1) и тепла (Q1):

ΔU1 = Q1 + W1
= 0 + W1
= W1

Процесс II:
- Начинаем в состоянии 2, где объем равен V2 и давление равно p2.
- Затем переходим в состояние 1, где объем равен V1 и давление равно p1.
- В этом процессе кривая является прямой линией.

Площадь под кривой процесса II равна:

W2 = p2 * (V1 - V2)

Определение тепла (Q2) в процессе II также должно быть дано в условии задачи. Предположим, что нам сказано, что процесс II является изобарным (Q2 = p2 * (V1 - V2)), то есть давление постоянно.

Таким образом, изменение внутренней энергии (ΔU2) в процессе II будет равно сумме работы (W2) и тепла (Q2):

ΔU2 = Q2 + W2
= p2 * (V1 - V2) + p2 * (V1 - V2)
= 2p2 * (V1 - V2)

Таким образом, изменение внутренней энергии при переходе газа из состояния 1 в состояние 2 при процессах I и II будет равно:

- Для процесса I: ΔU1 = W1
- Для процесса II: ΔU2 = 2p2 * (V1 - V2)

Необходимо знать точные значения объема и давления в состояниях 1 и 2, а также определение тепла (Q1 и Q2) для получения численных значений изменения внутренней энергии.