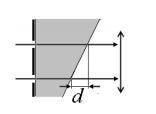
Одна сторона стеклянного клина закрыта экраном с двумя щелями, как показано на рисунке. На клин, перпендикулярно его поверхности, падает световой
пучок, который после прохождения клина собирается линзой. Длина падающей
волны x ; в стекле она меньше, и равна 2/3x. При какой разности толщины клина d около щелей интенсивность света в фокусе линзы будет максимальной?

Для решения этой задачи нам понадобятся знания о принципе интерференции света и о свойствах клина.

Принцип интерференции света гласит, что при наложении двух или более световых волн могут возникать так называемые интерференционные полосы - явление, при котором в некоторых местах свет усиливается, а в других - ослабевает.

При расчете разности хода световых лучей следует учитывать, что при прохождении через среды разной оптической плотности (в данном случае, воздуха и стекла) изменяется скорость света и, соответственно, длина волны.

Рассмотрим данную задачу по шагам.

1. Обозначим толщину клина d (около щелей) и длину падающей волны x.
2. Длина волны в стекле будет составлять 2/3x.
3. Пусть O1 и O2 - щели, расстояние между которыми равно D. Обозначим точку на фокусном расстоянии линзы как F.
4. Разность хода световых лучей от щелей O1 и O2 до фокуса F равна разнице оптических путей через клин, которая зависит от толщины клина d и лучевого наклона клина (угла i) в этом месте.
5. При равномерном распределении зон интерференции на клине будет наблюдаться максимум освещенности на фокусной плоскости линзы.
6. Для максимальных значений освещенности на фокусной плоскости, разность оптических путей от точек O1 и O2 до фокуса F должна быть целым числом полуволн длины x в стекле.
7. Полный оптический путь от точки O1 до точки F через клин равен d/cos(i).
8. Полный оптический путь от точки O2 до точки F через клин равен (d+D)/cos(180-i).
9. Разность оптических путей равна (d+D)/cos(180-i) - d/cos(i).
10. Для максимальной освещенности на фокусной плоскости, разность оптических путей должна быть целым числом полуволн длины x в стекле.
11. Упростим выражение (d+D)/cos(180-i) - d/cos(i):
(d+D)/cos(180-i) - d/cos(i) = (d+D)/(-cos(i)) - d/cos(i) = -D/cos(i).
12. Полуволна длины x в стекле равна полной длине волны x, так как длина волны в стекле равна 2/3x. То есть, x = 2/3x.
13. Выразим x через d и D: x = 2/3x, x = 2/3(2/3x), x = 4/9x.
14. Получили, что полуволновая длина x в воздухе равна 4/9x. Теперь, зная, что полуволновая длина должна быть равна разности оптических путей, найдем разность оптических путей, соответствующих максимальной освещенности.
15. Разность оптических путей равна -D/cos(i). Разность оптических путей должна быть целым числом полуволн длины 4/9x в воздухе:
-D/cos(i) = n * (4/9x), где n - натуральное число.
16. Решим это уравнение относительно D:
D = -n * (4/9) * x * cos(i).
17. Прикладывая законы геометрической оптики, можно показать, что sin(i) = n * (4/9).
18. Таким образом, для максимальной освещенности на фокусной плоскости линзы, разность толщины клина около щелей d должна быть такая, чтобы sin(i) = n * (4/9).
19. Зная, что sin(i) = n * (4/9), мы можем найти разность толщины клина около щелей d по закону преломления света на границе раздела стекло-воздух: n * sin(i) = (4/9)x.
20. Таким образом, разность толщины клина около щелей d должна быть равна (4/9)x.

Итак, в ответе на задачу мы получили, что разность толщины клина около щелей d должна быть равна (4/9)x, чтобы интенсивность света в фокусе линзы была максимальной.