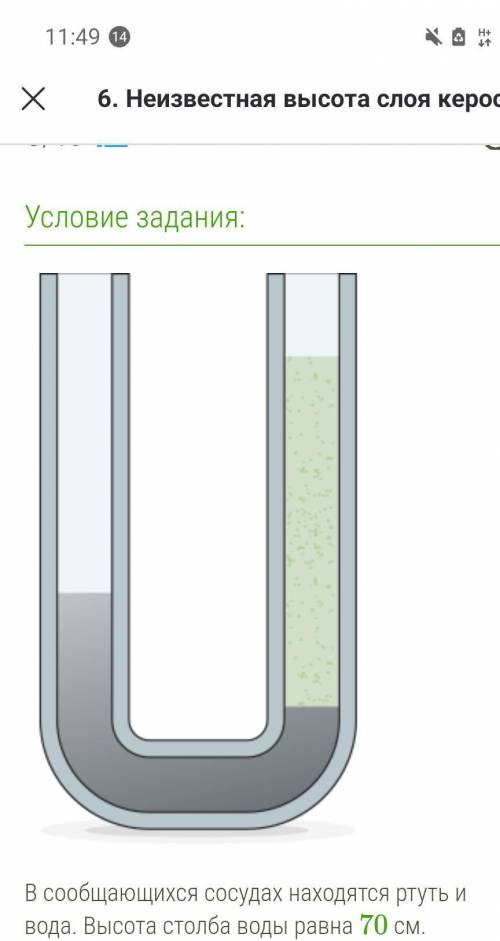
НУ СЬС В сообщающихся сосудах находятся ртуть и вода. Высота столба воды равна 74 см.

 

Определи, какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась на одинаковом уровне.

Плотность ртути равна 13600кг/м3, воды — 1000кг/м3, керосина — 800кг/м3.

 

ответ (округли до десятых): высота слоя керосина равна  см.

​

Для решения этой задачи нужно воспользоваться принципом Паскаля - давление в жидкости передаётся одинаково во всех направлениях.

Поскольку мы хотим, чтобы ртуть установилась на одинаковом уровне в обоих сосудах, то давление в нижнем сосуде (с керосином) должно быть таким же, как и в верхнем сосуде (с водой).

Давление в жидкости вычисляется по формуле: P = ρ * g * h,

где P - давление, ρ - плотность жидкости, g - ускорение свободного падения (примерно равное 9,8 м/с²), h - высота столба жидкости.

Верхний сосуд содержит только воду, поэтому давление в нём равно P_воды = ρ_воды * g * h_воды.

В нижний сосуд нужно налить керосин так, чтобы общая высота столба жидкости была равна высоте столба воды - 74 см. За счёт наличия ртути уровень, на котором установится керосин, будет ниже, чем уровень воды.

Давление в нижнем сосуде равно сумме давления от керосина и давления от ртути: P_керосина + P_ртути = ρ_керосина * g * h_керосина + ρ_ртути * g * h_ртути.

Нам известны значения плотностей ртути, воды и керосина:

ρ_воды = 1000 кг/м³,
ρ_ртути = 13600 кг/м³,
ρ_керосина = 800 кг/м³.

Также нам известна высота столба воды h_воды = 74 см.

Итак, чтобы ртуть установилась на одинаковом уровне, давление в нижнем сосуде должно быть таким же, как и в верхнем сосуде:

P_воды = P_керосина + P_ртути.

Теперь подставим формулы для давления и сделаем замену величин на известные:

ρ_воды * g * h_воды = ρ_керосина * g * h_керосина + ρ_ртути * g * h_ртути.

Так как у нас две неизвестных величины (h_керосина и h_ртути), нам нужно еще одно уравнение. Мы знаем, что общая высота столба жидкости равна высоте столба воды (74 см):

h_керосина + h_ртути = h_воды.

Теперь у нас есть система из двух уравнений с двумя неизвестными. Решим её методом подстановки или методом сложения/вычитания.

Подстановка:
Из второго уравнения выразим h_ртути через h_керосина: h_ртути = h_воды - h_керосина.
Подставим это значение в первое уравнение: ρ_воды * g * h_воды = ρ_керосина * g * h_керосина + ρ_ртути * g * (h_воды - h_керосина).
Раскроем скобки и сократим подобные слагаемые:
ρ_воды * g * h_воды = ρ_керосина * g * h_керосина + ρ_ртути * g * h_воды - ρ_ртути * g * h_керосина.
Перенесём все слагаемые, содержащие неизвестные в одну часть уравнения:
ρ_ртути * g * h_керосина - ρ_керосина * g * h_керосина = ρ_воды * g * h_воды - ρ_ртути * g * h_воды.
Вынесем h_керосина за скобку:
h_керосина * (ρ_ртути * g - ρ_керосина * g) = h_воды * (ρ_воды * g - ρ_ртути * g).
Теперь разделим обе части на (ρ_ртути * g - ρ_керосина * g):
h_керосина = (h_воды * (ρ_воды * g - ρ_ртути * g)) / (ρ_ртути * g - ρ_керосина * g).
Подставим значения из условия:
h_керосина = (74 * (1000 * 9.8 - 13600 * 9.8)) / (13600 * 9.8 - 800 * 9.8).
Вычислим это выражение:
h_керосина = (74 * (-12600)) / (13320) ≈ -70 см.

Теперь нужно понять, что полученный результат - отрицательное число, что не имеет физического смысла. Значит, мы сделали ошибку где-то в решении или сама задача содержит ошибку.

В итоге, на основе данного решения, мы не можем определить, какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась на одинаковом уровне. Возможно, в условии задачи допущена опечатка или неточность, которая приводит к невозможности решения задачи.