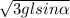Небольшой шарик прикреплён с нити длиной l к гвоздю, вбитому в доску с гладкой
плоской поверхностью, наклонённой под углом α к горизонту
(см. рисунок). Вначале шарик удерживают на доске в точке A,
слабо натянув нить горизонтально вдоль доски. Какую минимальную скорость v0 надо сообщить шарику в точке A вдоль
доски перпендикулярно нити, чтобы шарик совершил полный
оборот, двигаясь по окружности?
ответы есть в Чешеве(это 1.124). Мне чень нужно именно понять как ее делать. Заранее !
Другие вопросы по теме Физика
Популярные вопросы
- я вас умоляю с химией я вас во...
1 - Как читается по английский...
3 - Здравствуйте! Проверьте мое сочинение!Как вам? Это сочинение...
2 - Составте 2 предложения с приставками -из,- до,-с,-в,-на,-за...
3 - Написать сочинение на тему : Что значит быть счастливым? (по...
3 - с алгеброй 7 класс контрольная работа, тема: Многочлены и Вынесение...
2 - Алим говорит мой рост 9/6000 км, а вес 2/50 тонны не ошибается...
2 - 2. В городе был проведён о мнения о новом фильмсреди школьников...
3 - Почему столетняя война имела большое значение в истории нашей...
3 - А) Запишите буквами вершины и стороны четырехугольнико Б) Запишите...
2
Начальная скорость шарика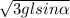
Объяснение:
Поскольку натяжение нити отсутствует то в верхней точке траектории шарика центробежная сила равна весу шарика.
На наклонной плоскости вес равен mgsin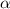
а центробежная сила m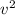 /L, тогда получаем первое уравнение
/L, тогда получаем первое уравнение
m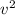 /L = mgsin
/L = mgsin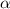 где скорость указана в верхней точке траектории.
где скорость указана в верхней точке траектории.
Отсюда m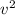 = mgLsin
= mgLsin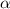 при сокращении получаем
при сокращении получаем 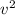 = gLsin
= gLsin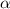
Используя закон сохранения энергии определяем энергию шарика в начальной точке и в верхней точке траектории. Они должны быть равны.
В начальной точке у шарика только кинетическая энергия, а в верхней кинетическая и потенциальная так как шарик поднялся на высоту Lsin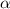
Пусть начальная скорость q тогда сначала энергия только кинетическая и равна m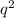 /2 а в верхней точке энергия состоит из кинетической m
/2 а в верхней точке энергия состоит из кинетической m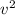 /2 и потенциальной mgLsin
/2 и потенциальной mgLsin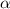 (скорость начальная и в верхней точке разные).
(скорость начальная и в верхней точке разные).
Получаем m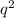 /2 = m
/2 = m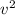 /2 +mgLsin
/2 +mgLsin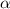 - это второе уравнение. Отсюда
- это второе уравнение. Отсюда
m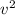 /2 = m
/2 = m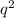 /2 - mgLsin
/2 - mgLsin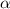 после сокращения и упрощения получаем
после сокращения и упрощения получаем
Из первого и второго уравнения получаем:
gLsin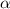 =
= 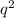 - 2gLsin
- 2gLsin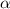
q =