1. Физика
  2. Небольшой шарик на нити

Небольшой шарик на нити движется по окружности в вертикальной плоскости. Найти массу шарика, если максимальное натяжение нити на ΔF=2,35 Н больше минимального.

Maksim55666 Maksim55666    2   30.08.2020 21:46    18

Ответы
akiceijuro akiceijuro  15.10.2020 16:28

39 г

Объяснение:

Пусть шарик вращается равномерно. Очевидно, наибольшего/наименьшего значения натяжение нити достигает в нижней/верхней точках траектории. Распишем втором закон Ньютона в проекции на вертикальную ось в этих точках (обязательно учтем, что скорость шарику внизу больше на величину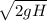 \displaystyle \sqrt{2gH}, где H=2R):

\displaystyle T_1-mg=ma_c= T_1-mg=\frac{mv^2}{R}+4mg

\displaystyle -T_2-mg=-\frac{mv^2}{R}

Выразим отсюда натяжения нитей:

\displaystyle T_1=\frac{mv^2}{R} +5mg

\displaystyle T_2=\frac{mv^2}{R}-mg

Их разность:

\displaystyle T_1-T_2=6mg=\Delta F

Откуда, искомая масса:

\displaystyle m=\frac{\Delta F}{6g}=\frac{2.35}{6*10}\approx0.039 кг или 39 г.


Небольшой шарик на нити движется по окружности в вертикальной плоскости. Найти массу шарика, если ма
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
anshul anshul  03.06.2019 09:40
Удельная теплоемкость стали 460 дж/кг °с. что это значит?...
vikaivanova12 vikaivanova12  03.06.2019 09:40
Какую работу выполняет двигатель автомобиля на пути 12 м,развивая силу тяги 5 кн?...
vlada051199 vlada051199  03.06.2019 09:40
Визначити поверхневу густину заряду,що створює поблизу поверні землі напруженість 200 в/м....
eva10072008mailru eva10072008mailru  03.06.2019 09:40
Два одинаковых тела имеют одинаковые заряды по модулю и разные по знаку. чему равны заряды этих тел, если при кратковременном соприкосновении от одного тела к другому перешло 10^20...
ПочтиОтличникМакс ПочтиОтличникМакс  31.08.2019 12:30
При какой температуре находится газ, если при нагревании его на 20 градусов при постоянном давлении объем увеличился в два раза? для каких газов это...
Nizam123 Nizam123  31.08.2019 12:30
Со дна реки глубиной 4 м поднимают камень объемом 0,6 куб.метров на поверхность.плотность камня 2500 кг/куб.метр,плотность воды 1000 кг/куб.метр.найти работу по подъёму камня....
yjtkf yjtkf  31.08.2019 12:30
Определите давление, который оказывает деревянный брусок на поверхность стола...
aruzhaan2003 aruzhaan2003  31.08.2019 12:30
Частица массой m, несущая заряд q, влетает в однородное магнитное поле с индукцией b со скоростью v и движется по окружности радиусом r. что произойдёт с радиусом орбиты и периодом...
krichilskaatтанюшка krichilskaatтанюшка  31.08.2019 12:30
Сила тяги сверхзвукового самолёта при скорости полёта 1240 км/ч равна 210 кн. найти мощность двигателей самолёта в этом режиме полёта....
10д 10д  31.08.2019 12:30
Удельной сопративление алюминия равно 0,028мком*м. определите сопративление проводника длиной 100 м и площадью поперечного сечения 2 мм2...

Популярные вопросы