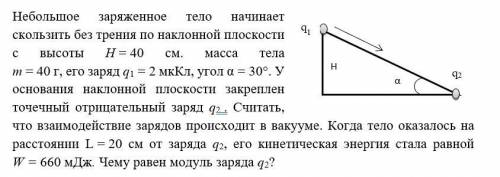
Небольшое заряженное тело начинает скользить без трения по наклонной плоскости с высоты Н = 40 см. масса тела m = 40 г, его заряд q1 = 2 мкКл, угол α = 30°. У основания наклонной плоскости закреплен точечный отрицательный заряд q2 . Считать, что взаимодействие зарядов происходит в вакууме. Когда тело оказалось на расстоянии L = 20 см от заряда q2, его кинетическая энергия стала равной W = 660 мДж. Чему равен модуль заряда q2?

Для начала рассмотрим силы, действующие на заряженное тело при его движении по наклонной плоскости.

1. Гравитационная сила: Fг = m * g * sinα, где m - масса тела, g - ускорение свободного падения, α - угол наклона плоскости.

2. Электростатическая сила: Fэ = k * q1 * q2 / r^2, где k - постоянная Кулона, q1 и q2 - заряды тел, r - расстояние между ними.

Найдем работу этих сил при перемещении тела от начального положения до точки L:

1. Работа гравитационной силы: Aг = m * g * sinα * L.

2. Работа электростатической силы: Aэ = -k * q1 * q2 / L.

По условию задачи, работа электростатической силы равна изменению кинетической энергии тела: Aэ = W = 660 мДж.

Таким образом, уравнение будет выглядеть следующим образом:

-к * q1 * q2 / L = 660 мДж

Для дальнейших расчетов, приведем все физические величины к СИ (метрической) системе, т.е.:

- модули зарядов q1 и q2 будут выражены в Кулонах (Кл),

- расстояние L будет выражено в метрах (м),

- работа W будет выражена в Джоулях (Дж).

Таким образом, переведем миллиджоули (мДж) в Джоули (Дж):

660 мДж = 660 * 10^-3 Дж = 0,66 Дж

Теперь мы можем записать уравнение в СИ системе:

-(k * q1 * q2) / L = 0,66 Дж

Подставим известные значения в уравнение:

-(9 * 10^9 Н * м^2 / Кл^2 * 2 * 10^-6 Кл * q2) / 0,2 м = 0,66 Дж

Упростим:

- 9 * 10^9 * 2 * 10^-6 * q2 / 0,2 = 0,66

- 9 * 10^9 * 2 * 10^-6 * q2 = 0,66 * 0,2

- 0,018 * 10^3 * q2 = 0,132

- q2 = 0,132 / (0,018 * 10^3)

Выполним необходимые расчеты:

q2 = 0,132 / 0,018 * 10^3

q2 = 7,33 * 10^-6 Кл

Таким образом, модуль заряда q2 равен 7,33 мкКл.