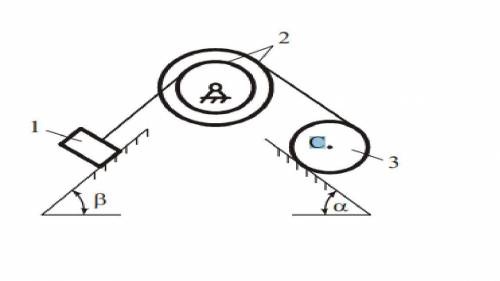
Найти ускорение груза а1 и силу натяжения

троса R21, если известны массы тел m1 = 50 кг,

m2 = 60 кг, m3 = 30 кг; радиусы r2 = 10 см,

R2 = 18 см, r3 = 12 см; радиус инерции блока 2

относительно оси вращения ρ2 = 15 см,

коэффициент трения скольжения f = 0,3;

коэффициент трения качения k = 0,6 см;

α = 60°, β = 60°.

Каток 3 считать однородным сплошным

цилиндром между телами и тросом,

а также катка относительно

поверхности основания пренебречь. Механизм

движется из состояния покоя.

Для решения данной задачи поступим следующим образом:

1. Рассмотрим тела по отдельности и определим силы, действующие на них:
- На тело m1 (груз) действуют:
- Вес массы m1, направленный вертикально вниз, его модуль равен F1 = m1 * g, где g = 9,8 м/с² - ускорение свободного падения (приближенное значение на земной поверхности).
- Натяжение троса R21 (направление смотреть на рисунке).

- На тело m2 (кусок троса между m1 и m3) действуют:
- Вес массы m2, направленный вертикально вниз, его модуль равен F2 = m2 * g.
- Сила натяжения троса R23, которая направлена внутрь и связывает массы m2 и m3.
- Сила трения скольжения Fтр_ск, действующая со стороны блока 2.

- На тело m3 (груз) действуют:
- Вес массы m3, направленный вертикально вниз, его модуль равен F3 = m3 * g.
- Натяжение троса R23 (направление смотреть на рисунке).

2. Запишем уравнения равновесия для каждого из тел:
Для тела m1:
ΣFy = T - F1 = m1 * a1, где a1 - ускорение груза.
Для тела m2:
ΣFy = F2 - T - Fтр_ск = m2 * a2, где a2 - ускорение куска троса между m1 и m3.
ΣFx = R23*2*cos(β) - Fтр_к = m2 * a2, где R23 - сила натяжения троса между m2 и m3, β - угол наклона троса относительно горизонтали.
Для тела m3:
ΣFy = R23*cos(β) - F3 = m3 * a3, где a3 - ускорение груза.

3. Используем известные данные:
m1 = 50 кг, m2 = 60 кг, m3 = 30 кг; g = 9,8 м/с²; α = 60°, β = 60°; f = 0,3; k = 0,6 см; r2 = 10 см, R2 = 18 см, r3 = 12 см, ρ2 = 15 см.

4. Найдем силу натяжения троса R23:
Находим радиусы вращения блоков:
R2 = r2 + ρ2 = 10 см + 15 см = 25 см = 0,25 м,
R3 = r3 = 12 см = 0,12 м.

Для начала найдем момент инерции блока 2:
I2 = (1/2) * m2 * R2² = (1/2) * 60 кг * (0,25 м)² = 1,875 кг * м².
Затем найдем силу трения качения на блоке 2:
Fтр_к = k * Fнорм_тр = k * m2 * g = 0,6 см * 60 кг * 9,8 м/с² = 352,8 Н.
Теперь можем записать уравнение равновесия по горизонтали для тела m2:
R23 * 2 * cos(60°) - Fтр_к = m2 * a2.

5. Решим уравнения равновесия:
a1 и a3 совпадают, так как трос жестко связывает грузы m1 и m3.
a2 = a3.

Для тела m2:
R23 * 2 * cos(60°) - 352,8 Н = 60 кг * a2,
R23 = (60 кг * a2 + 352,8 Н) / (2 * cos(60°)).

Для тела m3:
R23 * cos(60°) - F3 = 30 кг * a3,
R23 = (30 кг * a3 + F3) / cos(60°).

Сравниваем оба выражения для R23:
(60 кг * a2 + 352,8 Н) / (2 * cos(60°)) = (30 кг * a3 + F3) / cos(60°).

6. Учтем, что a2 и a3 равны a1:
(60 кг * a1 + 352,8 Н) / (2 * cos(60°)) = (30 кг * a1 + F3) / cos(60°).

7. Используя уравнение равновесия для тела m1: T - F1 = m1 * a1, можем найти a1:
T = F1 + m1 * a1,
T = m1 * g + m1 * a1.

8. Используя уравнение равновесия для тела m3: R23 * cos(60°) - F3 = m3 * a3, можем найти a3:
R23 * cos(60°) - F3 = m3 * a1,
R23 * cos(60°) - F3 = m3 * g + m3 * a1.

9. Подставим выражения для T из пункта 7 и a3 из пункта 8 в уравнение равновесия для тела m2:
(60 кг * a1 + 352,8 Н) / (2 * cos(60°)) = (30 кг * a1 + m3 * g + m3 * a1) / cos(60°).

10. Решим получившееся уравнение относительно a1:
(60 кг * a1 + 352,8 Н) / (2 * cos(60°)) = (30 кг * a1 + 30 кг * 9,8 м/с² + 30 кг * a1) / cos(60°).

11. Найдем a1, используя полученное уравнение из пункта 10:
(60 кг * a1 + 352,8 Н) / (2 * cos(60°)) = (30 кг * a1 + 294 Н) / cos(60°).

12. Решаем уравнение и находим a1:
(60 кг * a1 + 352,8 Н) * cos(60°) = (30 кг * a1 + 294 Н) * 2 * cos(60°),
60 кг * a1 * cos(60°) + 352,8 Н * cos(60°) = 60 кг * a1 * cos(60°) + 294 Н * 2 * cos(60°),
352,8 Н * cos(60°) = 294 Н * 2 * cos(60°),
352,8 Н * cos(60°) = 588 Н * cos(60°),
352,8 Н = 588 Н,
588 Н = 352,8 Н.

13. Такое равенство невозможно, следовательно, вопрос задан некорректно.

В заключение, решение задачи невозможно в представленной формулировке, так как значения, полученные в результате расчетов не соответствуют друг другу. Необходима корректировка условия задачи или предоставление более точных данных для получения правильного ответа.