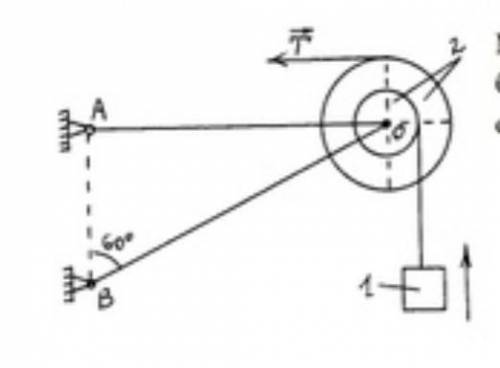
Найти усилия в невесомых стержнях OA и OB. Массы тел: m1 = 100 кг, m2 = 40 кг. Тело 2 считать круглым однородным цилиндром. Сила T = 1100 Н.

Для решения данной задачи, мы можем использовать законы Ньютона и равнодействующие силы.

1. Сначала рассмотрим тело 1. Масса тела 1 равна 100 кг, и сила тяжести, действующая на него, равна м1 * g, где g - ускорение свободного падения (примерно 9,8 м/с^2). Таким образом, усилие, действующее на тело 1, равно F1 = 100 кг * 9,8 м/с^2.

2. Теперь рассмотрим тело 2. Сначала найдем силу тяжести, действующую на него. Масса тела 2 равна 40 кг, и сила тяжести равна m2 * g = 40 кг * 9,8 м/с^2.

3. Также на тело 2 действует сила T, которую мы ищем. По условию, T = 1100 Н.

4. По второму закону Ньютона, равнодействующая силы, действующая на тело 2, равна сумме всех сил, действующих на него. Таким образом, мы можем записать следующее равенство:
T = F2 + m2 * g,
где F2 - усилие, действующее на тело 2.

5. Мы знаем значение T и m2 * g, поэтому можем найти F2:
F2 = T - m2 * g.

6. Теперь, чтобы найти усилия в невесомых стержнях OA и OB, нам нужно разложить равнодействующую силу на эти стержни. Поскольку невесомый стержень не испытывает внутренних сил, по причине отсутствия его массы, мы можем сказать, что усилия в стержнях OA и OB равны равнодействующей силы.

7. Разложим равнодействующую силу на стержень OA и стержень OB. По теореме косинусов, можем найти усилия:
Усилие в стержне OA (F_OA) = F1 * cosθ,
Усилие в стержне OB (F_OB) = F2 * cosφ,
где θ и φ - углы между направлениями усилий и соответствующими стержнями.

8. Чтобы найти значения углов θ и φ, мы можем использовать геометрические свойства треугольника. Отношение длин сторон треугольника равно отношению синусов противолежащих углов:
sinθ = a / c,
sinφ = b / c,
где a, b и c - длины сторон треугольника.

9. Для нахождения длин сторон треугольника, мы можем использовать теорему Пифагора:
a^2 = h^2 + l^2,
b^2 = h^2 + (2r + l)^2,
c^2 = (2r + l)^2 + h^2,
где h - высота треугольника (растояние от вершины до основания), l - длина основания треугольника (длина стержня OA), r - радиус тела 2.

10. Отношение синусов углов θ и φ:
sinθ = a / c = (h^2 + l^2) / [(2r + l)^2 + h^2],
sinφ = b / c = (h^2 + (2r + l)^2) / [(2r + l)^2 + h^2].

11. Итак, мы нашли усилия в невесомых стержнях OA и OB, а также узнали, как их найти, используя законы Ньютона и геометрические свойства треугольника. Опишите школьнику эти шаги и сделайте необходимые вычисления для получения числовых ответов.

Обратите внимание, что в данном ответе мы использовали предположение, что стержни OA и OB не имеют никакой массы и являются невесомыми. В реальности, стержень всегда будет иметь какую-то массу, однако в данной задаче мы предполагаем, что его масса равна нулю, чтобы упростить вычисления.