Найдите явный вид матриц-операторов компонент углового момента 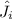 в состоянии с полным моментом
в состоянии с полным моментом 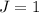
Другие вопросы по теме Физика
Популярные вопросы
- Вкаком слове разделительный мягкиц знак 1 кольцо 2 день 3 жилье 4...
2 - Выполни деление с остатком. сделай проверку. 42: 8 32: 5 61: 7 19:...
3 - Ғалымдар, электр, материал, құрылғы сөздерді қатыстырып сөйлемдер...
3 - Вследствие резкого тарможение пассажиры накланились вперёд. почему?...
1 - Первое кругосветное плавонье фернана магеллана а) 3 года б)4 года...
3 - По нормемаляр за 4 дня покрасил 48 парт..за сколько он выполнил бы...
2 - Определить силу тяжести действующую на латунный брусок если m=100г...
2 - Кпопуляционному взрыву численностей зайцев в лесу может превести :...
3 - Периметр равнобедренного треугольника равен 5,2 м найдите его стороны...
3 - Произведите подобные слагаемые: 2/3х-1/2х; 1/4х+1/3х; -7/12у-5/6у;...
1
Напомним основные свойства операторов углового момента с J=1
Введем повышающий и понижающий операторы
И вспомним их действие на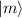
Чтобы найти коэффициенты, отметим, что
И поймем очевидное, что возможны лишь состояния с m=-1, 0, 1. Теперь мы можем понять, что
Теперь рассмотрим произвольное состояние
Действие на него оператора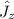 сводится к
сводится к
Оператор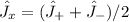 , поэтому
, поэтому
Аналогично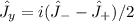 , поэтому
, поэтому