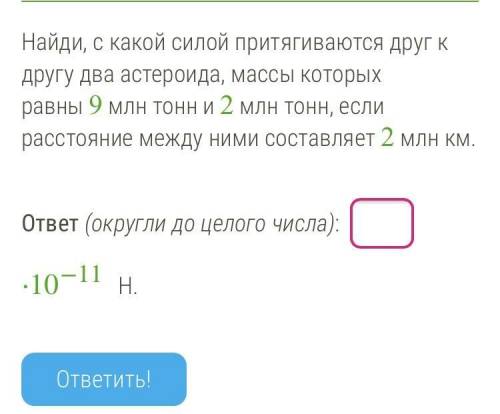
Найди, с какой силой притягиваются друг к другу два астероида, массы которых равны 9 млн тонн и 2 млн тонн, если расстояние между ними составляет 2 млн км
Другие вопросы по теме Физика
Популярные вопросы
- Как сделать ? дам за правильно...
2 - Биология пәнінен алған білімдеріңді пайдаланып фотосинтез процесі қалай жүретіні...
3 - Экологиялық сукцессия себеби не болып табылады?...
1 - 68.найдите значения выражений по действиям в столбик...
2 - X³=18 Распишите по действиям...
2 - Здравствуйте по химии практику На казахском......
1 - Тут у полонині де небо накриває бездонні простори що живуть у самотині тільки...
2 - Как составить рассказ по картинкам про грибы и два друзей.?...
3 - В фермерском хозяйстве в первый день было собрано 125 тонн картофеля во второй...
2 - Крастворт на тему уроки французского...
3
Закон гласит, что сила притяжения между двумя объектами прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Формула для вычисления силы притяжения:
F = G * (m1 * m2) / r^2
Где:
- F - сила притяжения между двумя телами,
- G - гравитационная постоянная, значение которой составляет G ≈ 6,674 * 10^(-11) Н*(м^2/кг^2),
- m1, m2 - массы двух тел,
- r - расстояние между телами.
Прежде чем вычислять силу притяжения, нам необходимо привести массы астероидов к килограммам, так как гравитационная постоянная указана в адекватных единицах измерения.
Масса первого астероида: 9 млн тонн = 9 * 10^6 тонн = 9 * 10^6 * 1000 кг = 9 * 10^9 кг
Масса второго астероида: 2 млн тонн = 2 * 10^6 тонн = 2 * 10^6 * 1000 кг = 2 * 10^9 кг
Теперь, когда у нас есть значения масс и расстояния, мы можем подставить их в формулу и вычислить силу притяжения:
F = G * (m1 * m2) / r^2
F = 6,674 * 10^(-11) * (9 * 10^9) * (2 * 10^9) / (2 * 10^6)^2
F = 6,674 * 9 * 2 * 10^(-11) * 10^9 * 10^9 / (2 * 10^6)^2
F = 120 * 10^(-2) N
F = 1,2 N
Таким образом, сила притяжения между двумя астероидами равна 1,2 Ньютона.