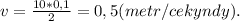1. Физика
  2. На тело находящееся в

На тело находящееся в состоянии покоя массой 2кг начинает действовать сила 10н. определить путь тела за 10с движения, скорость в конче 10 секунды

HFccv HFccv    2   18.05.2019 03:50    2

Ответы
True228228 True228228  11.06.2020 08:59

По формуле уравнения пути при равноускореном движении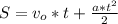 S=v_o*t+\frac{a*t^2}{2}, где t - промежуток времени, a - ускорение (м/с²), 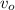v_o - начальная скорость (м/с).

По услвию задачи начальная скорость равна нулю, тогда формула пути прит вид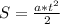 S=\frac{a*t^2}{2}. Так как тело начало двигатся по дейтсвие силы, то применяем второвй закон Ньютона 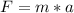F=m*a, где m - масса тела (кг), a - ускорение (м/с²).

Откуда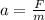 a=\frac{F}{m}. Данную формулу подставляем в формулу пути и получаем 

S=\frac{\frac{F}{m}*t^2}{2}=\frac{F*t^2}{2*m}. Подставляем численные данные и вычисляем S=\frac{10*10^2}{2*2}=250(metrov).

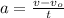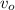В случае равноускоренного движения, ускорение даётся отношением изменения скорости к потребовавшемуся для этого времени т.е. a=\frac{v-v_o}{t}, где t - промежуток времени (с), v - конечная скорость (м/с), v_o - начальная скорость (м/с).

Так как начальная скорость равна нулю, то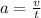 a=\frac{v}{t}. Отсюда скорость равна 

v=a*t, ускорение есть a=\frac{F}{m}, то v=\frac{F}{m}*t=\frac{F*t}{m}

Промежут времени равен конец 10-ой секунде, если общее время движения равно 10 секунд то конец десятой секунды равен 0,1 с. Подставляем и вычисляем: v=\frac{10*0,1}{2}=0,5(metr/cekyndy).

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
Victoriya1234567890 Victoriya1234567890  29.04.2020 12:58
Рассчитайте и постройте механическую характеристику Мс (ω) вентилятора с учетом моментов потерь в двигателе ∆Мдв и механизме ∆Мм. Рв.н, кВт=10 ωв.н. , 1/с=314 ∆Мдв, Нм=5 ∆Мм,...
Страус123552 Страус123552  29.04.2020 12:58
Плечи рычага отличаются в два раза L1 = 1м, L2 = 2м. С рычага нужно поднять камень массой 50 кг. Какую силу нужно приложить к большему плечу рычага? На сколько опустится большее...
ник4858 ник4858  17.06.2019 12:00
Уравнения движения тела имеет вид: x=3t+3t^2. определить импульс тела через 10 сек после начала движения, если масса тела 10 кг...
3Человек3 3Человек3  17.06.2019 12:00
Автомобиль с двигателем мощностью 100 квт за 1 час потребляет 30 л бензина. каков кпд двигателя автомобиля? плотность бензина равна 710 кг/м3. по этапно решите,...
fvbh3fvhc fvbh3fvhc  26.09.2019 03:50
Сопротивление в цепи увеличилось в 2 раза.как изменится сила тока если напряжение осталось прежним...
Вероніка200419 Вероніка200419  26.09.2019 03:50
Как изменится сила тока, проходящего через проводник, если увеличить в 2 раза напряжение между его концами, а длину проводника уменьшить в два раза...
Ankur1 Ankur1  26.09.2019 03:50
23,5 длина шагов 17 шагов за 10 секунд как найти пройденный путь 90 !...
sashadorosh1953 sashadorosh1953  26.09.2019 03:50
На расстоянии l = 56 см от своего действительного изображения расположен предмет. определи расстояние от линзы до предмета, если изображение больше предмета в n= 2,2 раз(-а)....
АРТЕМІДА555 АРТЕМІДА555  26.09.2019 03:50
Взаимное гравитационное влияние земли и луны выражается: а/ в наличии приливных сил б/ в том, что луна обращена к земле одной стороной в/ в том, что на луне нет атмосферы...
vadimtolpegin vadimtolpegin  21.09.2019 23:30
Зачем в банковской карточке магнитная лента?...

Популярные вопросы