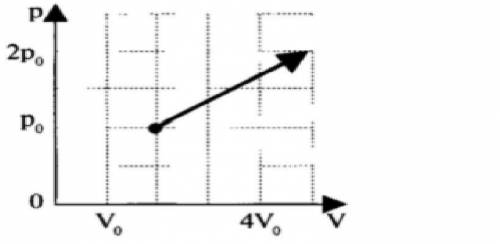
На рV — диаграмме изображен процесс перевода газа, совершенный с одним молем идеального одноатомного газа. Чему равно количество теплоты, переданное газу при переходе из состояния 1 в состояние 2? р0 = 0,1 МПа, V0 = 2 л.

Для решения данной задачи нам необходимо воспользоваться формулой для вычисления количества теплоты, переданного газу:

Q = Cv ΔT

где Q - количество теплоты, переданное газу, Cv - молярная удельная теплоемкость газа при постоянном объеме, ΔT - изменение температуры газа.

Дано, что газ является идеальным одноатомным газом. Для такого газа молярная удельная теплоемкость при постоянном объеме выражается как Cv = (3/2)R, где R - универсальная газовая постоянная.

Также дано, что процесс перевода газа из состояния 1 в состояние 2 представлен на рV-диаграмме. Из диаграммы видно, что процесс представляет собой изобарное сжатие газа.

Используя известные значения и формулы, приступим к решению задачи.

1. Определим начальное и конечное давление газа.
Из условия задачи известно, что р0 = 0,1 МПа (мегапаскали) - начальное давление газа.

На рV-диаграмме видно, что состояние 2 соответствует точке с координатами (3л, 0,04МПа). Это значит, что конечное давление газа равно 0,04 МПа.

2. Определим начальный и конечный объем газа.
Из условия задачи известно, что V0 = 2 л (литра) - начальный объем газа.

На рV-диаграмме видно, что состояние 2 соответствует точке с координатами (3л, 0,04МПа). Это значит, что конечный объем газа равен 3 л.

3. Определим изменение температуры газа.
Мы знаем, что процесс представляет собой изобарное сжатие газа. По определению изобарного процесса, давление газа остается постоянным.

ΔT = T2 - T1

В идеальном газе изменение температуры связано с изменением объема. Так как у нас дано изобарное сжатие, то температура газа пропорционально изменяется с объемом.

ΔT = (V2 - V1) / V0 * T0

ΔT = (3 л - 2 л) / 2 л * T0

ΔT = (1 л) / 2 л * T0

ΔT = 0,5T0

4. Подставим известные значения в формулу для вычисления количества теплоты:

Q = Cv ΔT

Q = (3/2)R * 0,5T0

В данной задаче мы не знаем температуру газа, но нам дана возможность найти ее, воспользовавшись уравнением состояния идеального газа:

PV = nRT

где P - давление газа, V - объем газа, n - количество вещества (моль), R - универсальная газовая постоянная, T - температура газа.

Для одноатомного идеального газа число степеней свободы равно 3. Используя это, мы можем выразить температуру газа через начальное давление и объем:

T0 = (P0 * V0) / (nR / F)

T0 = (0,1 МПа * 2 л) / (1 моль * 8,314 Дж/(моль*К) / 3)

T0 = (0,2 МПа * 3 л) / (8,314 / 3)

T0 = (0,6 MPa * l) / (8,314 / 3)

T0 = (0,6 MPa * l) / (2,771333333333333)

T0 ≈ 0,216 К

Подставим найденное значение температуры в формулу для вычисления количества теплоты:

Q = (3/2)R * 0,5 * 0,216 К

Q ≈ (3/2) * 8,314 Дж/(моль*К) * 0,108 Дж/моль

Q ≈ 0,162 Дж

Таким образом, количество теплоты, переданное газу при переходе из состояния 1 в состояние 2, примерно равно 0,162 Дж.