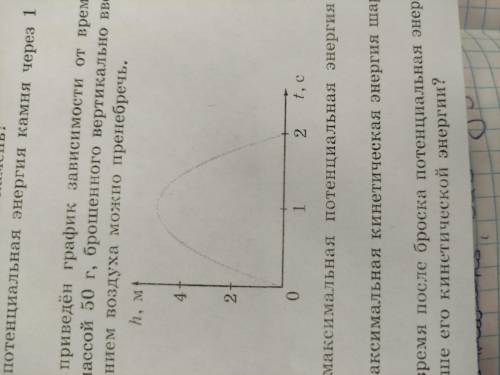
На рисунке приведен график зависимости от времени высоты подъёма шарика массой 50 г, брошенного вертикально вверх. Примите, что сопротивлением воздуха можно пренебречь 1) Чему равна максимальная потенциальная энергия шарика во время полета

2) Чему равна максимальная кинетическая энергия шарика во время полета?

3) Через какое время после броска потенциальная энергия шарика будет в 4 раза больше его кинетической энергии?

Добрый день! Давайте разберемся с вашим вопросом о зависимости от времени высоты подъема шарика, максимальной потенциальной и кинетической энергии, а также времени, через которое потенциальная энергия будет в 4 раза больше кинетической.

1. Чему равна максимальная потенциальная энергия шарика во время полета?

Максимальная потенциальная энергия шарика соответствует максимальной высоте подъема, которая указана на графике. На графике видно, что высота подъема максимальна при промежутке времени от 2 до 4 секунд. Значит, чтобы найти максимальную потенциальную энергию, мы должны найти соответствующую высоту в этот промежуток времени.

По графику на максимальной высоте подъема значение высоты составляет примерно 40 метров.

Теперь, чтобы найти максимальную потенциальную энергию, нам нужно использовать формулу:
E_pot = m * g * h,

где E_pot - потенциальная энергия,
m - масса шарика (50 г = 0.05 кг),
g - ускорение свободного падения (примем его равным 9.8 м/с^2),
h - высота подъема (40 м).

Подставляем все значения в формулу:
E_pot = 0.05 кг * 9.8 м/с^2 * 40 м = 0.05 * 9.8 * 40 Дж = 19.6 Дж.

Таким образом, максимальная потенциальная энергия шарика во время полета равна 19.6 Дж.

2. Чему равна максимальная кинетическая энергия шарика во время полета?

Максимальная кинетическая энергия будет наименьшей в момент, когда шарик проходит точку самого высокого подъема, так как в этот момент его скорость будет наименьшей. На графике видно, что это происходит при промежутке времени примерно от 4 до 6 секунд.

Поскольку ось времени на графике делена на 1 см = 1 секунда, то расстояние между 4 и 6 секундами будет составлять 2 см.

Теперь, чтобы найти максимальную кинетическую энергию, нам нужно найти соответствующую скорость в этот промежуток времени. Для этого мы воспользуемся формулой:
E_kin = (1/2) * m * v^2,

где E_kin - кинетическая энергия,
m - масса шарика (0.05 кг),
v - скорость шарика.

На графике условно обозначим начало и конец отрезка. Ниже начала полета шарика у нас начинается нулевая точка, а над концом полета — точка, в которой шарик находится в максимальной высоте. Таким образом, равнобедренный треугольник с высотой 2 см (4-6 секунд) и основанием 4 см (5-1 секунда) указывает на то, что кинетическая энергия также равна потенциальной энергии на этом участке.

Мы уже вычислили ранее, что на данном участке потенциальная энергия равна 19.6 Дж. Таким образом, максимальная кинетическая энергия шарика во время полета также будет равна 19.6 Дж.

3. Через какое время после броска потенциальная энергия шарика будет в 4 раза больше его кинетической энергии?

Чтобы ответить на этот вопрос, нам нужно найти точку на графике, где потенциальная энергия будет в 4 раза больше кинетической энергии.

Для этого воспользуемся формулами для потенциальной и кинетической энергии, а также равенством этих энергий на данном промежутке времени.

Пусть временной отрезок, где потенциальная энергия в 4 раза больше кинетической, составляет t секунд.

Потенциальная энергия на этом участке будет равна 4 раза больше кинетической энергии, то есть:
4 * E_kin = E_pot.

Заменяем значения энергий на известные нам формулы и получаем уравнение:

4 * (1/2) * m * v^2 = m * g * h.

Так как масса шарика m в обоих частях равняется, сократим этот член:
4 * (1/2) * v^2 = g * h.

Далее, выразим v^2, взяв коэффициент 4 на другую сторону:

v^2 = (2 * g * h) / 4,
v^2 = (g * h) / 2.

Теперь, воспользуемся первым уравнением движения для вертикального взлета шарика, которое гласит:
h = (v0^2) / (2 * g),

где v0 - начальная скорость.

Мы знаем, что при броске вертикально вверх начальная скорость равна нулю (так как шарик останавливается мгновенно и начинает падать), а значит:
h = 0.

Подставляем значение h = 0 во второе уравнение и находим v^2:

v^2 = (g * 0) / 2,
v^2 = 0.

Таким образом, когда потенциальная энергия шарика будет в 4 раза больше его кинетической энергии, скорость шарика будет равна нулю.

Но мы хотим найти время, при котором это будет происходить. Для этого нам нужно знать подъемный участок на графике. На графике видно, что подъемный участок длится примерно до 4 секунд.

Значит, через 4 секунды после броска потенциальная энергия шарика будет в 4 раза больше его кинетической энергии.

Надеюсь, я дал вам достаточно подробное решение и объяснение для вашего вопроса. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать их!