На рисунке представлен график зависимости скорости X автомобиля от времени t найдите путь пройденный автомобилем за 5 секунд, ответ обоснуйте
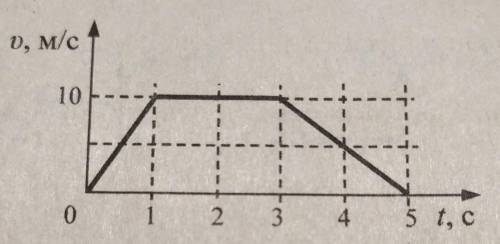
Другие вопросы по теме Физика
Популярные вопросы
- Сглавными членами предложения разобраться. после экзамена нам с отцом...
3 - С7 класс. учебник в. в. казакова 2017год.№155 на биссектрисе угла авс...
2 - Решите и распишите как делали 6 целых 2/9- 3 целых 6/7...
2 - Сравнительная таблица кольчатых и членистоногих...
3 - Найдите приближённое произведения профлист множители до самой высокой...
2 - Родственные слова с приставками и частицей -ся смотреть видеть ненавидеть...
1 - Сочинение по поэме мцыри план: 1. о поэме 2. образ мцыри: мальчика попавшего...
2 - Дайте определения словам : зодчество хоры ,алтарь ,купол ,паперть...
3 - Фактор влияющий на процесс горообразования?...
1 - За 2 дня пропололи 7/9 огорода причём в первый день пропололи 5/9 огорода...
2
Однако, на графике представлена зависимость скорости от времени, и нам нужно найти путь. Для этого нам необходимо найти площадь под графиком.
Для начала разобьем область под графиком на несколько частей. Разделим ее на две треугольные области и одну прямоугольную область.
Область первого треугольника: основание треугольника равно 2 секунды, а высота составляет 10 м/с. Поэтому площадь первого треугольника равна (1/2) * 2 * 10 = 10 м.
Область второго треугольника: основание треугольника равно 3 секунды, а высота составляет 5 м/с. Поэтому площадь второго треугольника равна (1/2) * 3 * 5 = 7.5 м.
Область прямоугольника: ширина прямоугольника равна 2 секунды (от 5 до 7 секунд), а высота составляет 5 м/с. Поэтому площадь прямоугольника равна 2 * 5 = 10 м.
Теперь найдем сумму площадей этих трех областей: 10 + 7.5 + 10 = 27.5 м.
Таким образом, автомобиль прошел путь в 27.5 м за 5 секунд.
Такой ответ обоснован, потому что мы использовали определение пути и разбили площадь под графиком на несколько геометрических фигур, найдя площади каждой из них и сложив их вместе. Это позволяет нам найти путь, пройденный автомобилем за данное время.