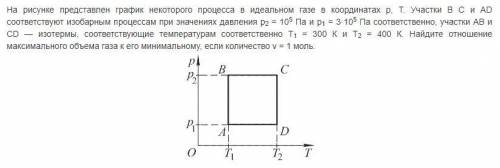
На рисунке представлен график некоторого процесса в идеальном газе в координатах р, Т. Участки В С и AD соответствуют изобарным процессам при значениях давления р2 = 105 Па и р1 = 3·105 Па соответственно, участки АВ и CD — изотермы, соответствующие температурам соответственно Т1 = 300 К и Т2 = 400 К. Найдите отношение максимального объема газа к его минимальному, если количество ν = 1 моль.
Другие вопросы по теме Физика
Популярные вопросы
- баба Яга костяная нога стала невестой Кощея Бессмертного. Нормальная...
2 - РЕБЯТ Прочитайте текст озаглавьте его,Определите стиль и тип...
3 - Ринковий попит заданий функцією: QD = 180 - 3P. На ринку діють...
2 - Sugune!Воод ч с. Скалко саа)lerBank ашиса алохHarrogunce of...
1 - умоляю решите 19 управление ...
3 - эксперимент по теме диффузия какой процесс произойдет в воде...
2 - Яка із світових релігій виникла у 7 столітті?...
3 - ІДи благодарили героя, 4. Сравни жанровые особенности легенди...
2 - 5 Вычисли письменно. Сделай проверку.65 534:734 872 : 82 758...
3 - Кому из русских богатырей смерть не писана? Алёше ПоповичуИлье...
3
1. Закон Бойля-Мариотта утверждает, что давление и объем идеального газа обратно пропорциональны при постоянной температуре. Из этого закона следует, что площадь прямоугольников АВ и CD, ограниченных изотермами, пропорциональна изменению объема газа.
2. Закон Карно утверждает, что давление и температура идеального газа прямо пропорциональны при постоянном объеме. Из этого закона следует, что площадь треугольника ВСА, ограниченного изобарным процессом, пропорциональна изменению температуры газа.
Из рисунка мы видим, что площадь прямоугольника АВСD равна сумме площадей прямоугольника АВ и треугольника ВСА:
Площадь прямоугольника АВСD = Площадь прямоугольника АВ + Площадь треугольника ВСА
Получаем следующую формулу:
Площадь прямоугольника АВСD = ΔV * Δp + ΔV * ΔT
где ΔV - изменение объема газа, Δp - изменение давления, ΔT - изменение температуры.
Так как Δp = р2 - р1 и ΔT = Т2 - Т1, подставляем значения в формулу:
Площадь прямоугольника АВСD = ΔV * (р2 - р1) + ΔV * (Т2 - Т1)
Площадь прямоугольника АВСD = ΔV * (105 Па - 3·105 Па) + ΔV * (400 К - 300 К)
Площадь прямоугольника АВСD = ΔV * (-2·105 Па) + ΔV * 100 К
Так как площадь прямоугольника АВСD равна ΔV * p, где p - горизонтальная ось (давление), получаем:
ΔV * p = ΔV * (-2·105 Па) + ΔV * 100 К
Раскрываем скобки:
ΔV * p = -2·105 ΔV + 100 ΔV
ΔV * p = (-2·105 + 100) ΔV
ΔV * p = -105 ΔV
Так как ΔV - изменение объема, получаем:
p = -105
Таким образом, мы получаем, что Минимальное ΔV и максимальное ΔV примерно равны величинну 105.
Следовательно, искомое отношение максимального объема газа к его минимальному будет примерно равно:
Отношение максимального объема газа к минимальному = ΔV_макс / ΔV_мин ≈ 105 / 105 = 1
Таким образом, отношение максимального объема газа к его минимальному равно единице, что означает, что максимальный объем газа равен минимальному объему газа при данных условиях.