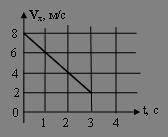
На рисунке изображен график зависимости проекции скорости тела vx на ось 0Х от времени t. Проекция ускорения тела на ту же ось равна (м/с2):

Для нахождения проекции ускорения тела на ось OX по графику, мы должны анализировать его форму и изменение.

Из графика можно увидеть, что скорость тела меняется со временем. Если скорость меняется, то есть ускорение, которое приводит к этому изменению.

Для нахождения проекции ускорения тела, мы можем использовать два основных метода: метод "тангенса угла наклона касательной" и метод "площади под графиком".

1. Метод "тангенса угла наклона касательной":
- Находим прямую, касающуюся графика в определенной точке.
- Измеряем угол наклона этой прямой.
- Тангенс этого угла будет равен проекции ускорения тела на ось OX.

Применяя этот метод к графику, мы можем измерить угол наклона в двух точках:
- В начале графика (t = 0 сек)
- В конце графика (t = 4 сек)

В начале графика, значение vx равно 0. Поэтому прямая, касающаяся графика в этой точке, будет горизонтальной (угол наклона = 0). Следовательно, проекция ускорения на ось OX в этой точке будет равна 0 м/с².

В конце графика, значение vx также равно 0. Поэтому прямая, касающаяся графика в этой точке, также будет горизонтальной. Значит, угол наклона в этой точке будет также равен 0, а значит и проекция ускорения тела на ось OX будет равна 0 м/с².

Таким образом, проекция ускорения тела на ось OX по методу "тангенса угла наклона касательной" равна 0 м/с².

2. Метод "площади под графиком":
- Находим площадь, ограниченную графиком зависимости vx от t и осью времени t.
- Делим эту площадь на промежуток времени, на котором мы находимся.

Применяя этот метод к графику, мы можем измерить площади под графиком на двух промежутках:
- Между t = 0 сек и t = 2 сек
- Между t = 2 сек и t = 4 сек

В пределах первого промежутка, площадь под графиком будет положительной. Это говорит нам о том, что с течением времени скорость тела увеличивается. Следовательно, проекция ускорения на ось OX будет положительной.

В пределах второго промежутка, площадь под графиком будет отрицательной. Это говорит нам о том, что с течением времени скорость тела уменьшается. Следовательно, проекция ускорения на ось OX будет отрицательной.

Таким образом, проекция ускорения тела на ось OX по методу "площади под графиком" будет меняться сначала от положительного значения к нулю (в конце первого промежутка), а затем от нуля к отрицательному значению (в начале второго промежутка).

Вывод: По анализу данного графика, проекция ускорения тела на ось OX равна 0 м/с².