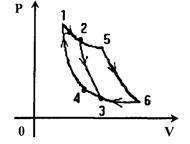
На рисунке 1-2-5 изотерма, 6-3-4 - изотерма, 2-3, 5-6, 4-1 - адиабаты. Рас-сматриваются 2 цикла: I - 12341, II - 15641. Какое из соотношений для КПД циклов справедливо? 1) КПД1 = КПД2 = 0
2) КПД1 = КПД2
3) КПД1 = КПД2 = 
4) КПД1 > КПД2
5) КПД1 < КПД2

Для решения этого вопроса, нам необходимо понять, что такое КПД (коэффициент полезного действия) и как он связан с графиками изотерм и адиабат.

КПД цикла обычно определяется как отношение работы, совершаемой системой к полученной системой теплоты. В данном случае, так как изотермы помечены цифрами 1, 2 и 5, а адиабаты - цифрами 2, 3, 4, 5 и 6, мы можем сделать вывод, что циклы I и II это замкнутые кривые, проходящие через данные точки.

КПД цикла можно рассчитать как 1 минус отношение работы вне цикла к суммарной подводимой системой теплоте. Для вычисления работы, нужно найти площадь, ограниченную циклом на оси давления и объема. Для удобства мы можем разбить цикл на изотермы и адиабаты, и рассчитывать площади каждой из этих фигур.

Давайте рассмотрим цикл I: 12341

- Между 1 и 2 у нас есть адиабата, значит работа совершается при изменении давления и объема между этими точками. Учитывая, что адиабаты у нас наклонные линии, мы можем рассчитать площадь треугольника, образованного этой адиабатой и осями давления и объема.

- Затем, между 2 и 3 у нас есть изотерма. Изотерма - это прямая горизонтальная линия на графике, и площадь под ней рассчитывается как прямоугольник на графике давления и объема.

- Между 3 и 4 снова адиабата, и мы можем рассчитать площадь треугольника.

- Наконец, между 4 и 1 у нас снова изотерма.

Теперь мы можем рассчитать работу внутри цикла I, сложив площади всех этих фигур. Делаем то же самое для цикла II: 15641.

Когда мы получим работы циклов I и II, мы сравниваем их и рассчитываем КПД циклов, используя формулу 1 минус отношение работы вне цикла к подводимой теплоте.

Теперь осталось только определить, какое из соотношений КПД справедливо.

Пошаговые решения и расчеты мы выполнять письменно, но чтобы система могла принимать ответ, нужно выбрать один из предложенных вариантов.

На рисунке дана только одна температура, значит это не процесс изоэнтропии, значит система не идеальна. Из этого можно сделать вывод, что степень свободы газа меняется на входе и выходе из системы. Поэтому КПД1 и КПД2 можно сравнить и определить, какой из них больше или меньше. Ответы "КПД1 > КПД2" или "КПД1 < КПД2" подходят для этой ситуации.

Ответ: В данном случае мы не можем утверждать, что КПД1 = КПД2 или КПД1 = КПД2 = . Мы можем только сказать, что КПД1 > КПД2 или КПД1 < КПД2. Ответы 4) КПД1 > КПД2 и 5) КПД1 < КПД2 являются верными для этого вопроса.