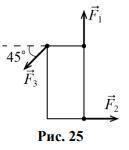
На прямоугольную пластину (рис. 25) в её плоскости действуют силы F1=F2=20 H, F3=20√2 H. Покажите, что у такой системы сил нет равнодействующей. Опишите качественно начальный характер движения пластины под действием этих сил из неподвижного состояния.

Добрый день! Давайте рассмотрим эту задачу по порядку.

Сначала давайте определим равнодействующую силу. Равнодействующая сила - это сумма всех действующих на пластину сил. В данном случае, у нас действуют три силы: F1, F2 и F3.

F1 = F2 = 20 H, а F3 = 20√2 H.

Для начала, давайте сложим силы F1 и F2. Так как они равны по величине и направлены в противоположные стороны, их векторные суммы компенсируют друг друга, и равняются нулю.

F1 + F2 = 20 H + (-20 H) = 0 H

Теперь давайте рассмотрим силу F3. Она направлена вдоль одной из диагоналей пластины и имеет величину 20√2 H.

Таким образом, сумма всех сил равна:

F1 + F2 + F3 = 0 H + 20√2 H = 20√2 H

Мы получили ненулевое значение суммы сил, следовательно, у данной системы сил есть равнодействующая, которая равна 20√2 H.

Теперь приступим к описанию начального характера движения пластины под действием этих сил из неподвижного состояния.

Изначально пластина находится в неподвижном состоянии, что означает, что сумма всех сил, действующих на неё, должна быть равна нулю.

Однако, в данном случае, мы видим, что сумма сил не равна нулю и составляет 20√2 H. Это означает, что на пластину действует неравновесная сила и она будет приобретать некоторое ускорение.

Качественно, начальное движение пластины будет характеризоваться ускорением в направлении, соответствующему суммарной силе F3. Так как F3 направлена вдоль одной из диагоналей пластины, она будет вызывать у пластины движение в этом направлении. В зависимости от условий задачи, пластина может начать двигаться вдоль этой диагонали или начнет вращаться вокруг своей оси.

Надеюсь, ответ был понятен и полезен! Если у вас есть еще вопросы, пожалуйста, задавайте!