На оси ox в точке х1=0 находится оптический центр тонкой рассеивающей линзы с фокусным расстоянием -30 см, а в точке х2=30 см - тонкой собирающей линзы с фокусным расстоянием 30 см. на рассеивающею линзу по оси ox падает параллельный пучок света из области x< 0. найдите координату х точки (в см), в которой собирается этот пучок, пройдя оптическую систему
Другие вопросы по теме Физика
Популярные вопросы
- 1.Ребята, посмотрите на карту Казахстана и подумайте в какой местности водная...
3 - із точки до площини проведено дві похилі які мають довжини 10 см і 17 см...
1 - Какие 2 документа в нашей стране (Казахстан) обеспечивают свободу вероисповедания?...
3 - Work in pairs. Imagine you went on a trip with a friend and some things...
2 - Задание 1. Внимательно посмотри на картинки. a) В каком регионе развиты...
2 - Приведите примеры (не менее двух) изменений в области образования...
1 - Берілген сөйлемдердің түбірі мен қосымшасын ажыратып, морфологиялық талдау...
1 - ЭТО СОР , задание на фото ...
1 - The eruption of the Krakatau (or Krakatoa) on a small island located in...
1 - на одной полке книг в 2 раза больше чем на другой всего на двух полках 60...
1
Дано:
x₁=0 см;
F₁=-30 см;
x₂=30 см;
F₂=30 см;
__________
Найти: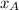
Изобразим ход лучей в данной оптической системе (см. рисунок).
Заметим, что рассеивающая линза дает пучок расходящихся лучей, продолжение которых сходится в точке x=-30 см, значит рассеивающую линзу можно отбросить, заменив ее фиктивным точечным источником света, расположенным в точке с координатой -30 см. Применив такой подход, мы получили систему состоящую только из собирающей линзы. Рассчитаем искомую координату, воспользовавшись формулой тонкой линзы:
Выразим координату точки пересечения световых лучей:
Выполним подстановку и расчет:
ответ: 90 см.