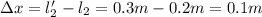На одном из концов горизонтального стержня длиной 1,2 м и массой 10 кг подвешен груз массой 20 кг. Стержень имеет одну точку опоры и находится в равновесии. а) Чему равна сила натяжения троса?
б) На каком расстоянии от конца стержня находится точка опоры?
в) На сколько надо передвинуть точку опоры, чтобы стержень остался в равновесии, если увеличить массу груза в 2 раза?

Ответы

Легендабокса 12.06.2021 20:31

Объяснение:

ДАНО:

$l = 1.2 m\\m = 10kg\\M = 20 kg\\ g = 10 m/c^2$

-----------------------------

1) Не очень понятно, что есть трос, но, вероятно, он соединяет груз и стержень. Тогда сила натяжения по 2 зак. Ньютона будет равна силе тяжести груза:

T = Mg

T = 20kg * 10m/c^2

T = 200H

2) Так как сила тяжести стержня должна прикладываться к центру масс, а он располагается посередине стрежня. Вспомним правило моментов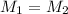 M_1=M_2 , согласно которому произведение сил на их плечи должны быть равны (силы тяжести стержня и силы натяжения троса).

$M_1 = Fl_1\\M_2 = Tl_2$

Так как сила тяжести стержня равна

$F = mg\\F = 10kg*10m/c^2 = 100H$

А это в два раза меньше меньше силы натяжения, то плечо силы тяжести должно быть в два раза больше плеча силы натяжения. Если точка опоры стоит по одну сторону от центра и края, где весит груз, то плечо силы тяжести всегда меньше плеча силы натяжения. Значит, точка опоры лежит между центром и краем. Данное расстояние равно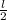 $\frac{l}{2}$ . Тогда имеем систему уравнений:

$\left \{{l_1+ l_2=\frac{l}{2}}\atop{l_1=2l_2}} \right.$

Решения ее:

$l_1= \frac{l}{3} = \frac{1.2m}{3} =0.4m \\\\l_2= \frac{l}{6} =\frac{1.2m}{6} = 0.2 m \\$

Тогда расстояние от конца, где прикреплен груз, равно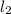 l_2 - равно 0,2м. Расстояние от другого конца это l - l_2 = 1м

3)Решение аналогично пункту 2:

Так как сила тяжести стержня должна прикладываться к центру масс, а он располагается посередине стрежня. Вспомним правило моментов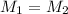 M_1=M_2 , согласно которому произведение сил на их плечи должны быть равны (силы тяжести стержня и силы натяжения троса).

$M'_1 = F'l'_1\\M'_2 = Tl'_2$

Так как сила тяжести стержня равна

$F' = 2mg\\F' = 2*10kg*10m/c^2 = 200H$

А это численно равно силе натяжения, следовательно, плечо силы тяжести должно быть равно плечу силы натяжения. Если точка опоры стоит по одну сторону от центра и края, где весит груз, то плечо силы тяжести всегда меньше плеча силы натяжения. Значит, точка опоры лежит между центром и краем. Данное расстояние равно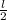 $\frac{l}{2}$ . Тогда имеем систему уравнений:

$\left \{{l'_1+ l'_2=\frac{l}{2}}\atop{l_1'=l_2'}} \right.$