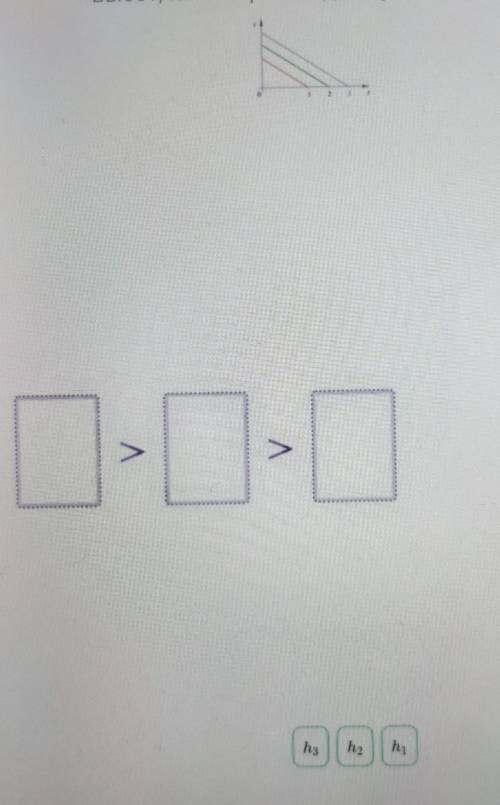
На графике показана зависимость скорости от времени для трех тел , брошенных вертикально . составьте неравенство для максимальных высот на которые поднимутся эти тела​

Чтобы составить неравенство для максимальных высот, на которые поднимутся эти тела, нужно знать, как скорость связана с высотой.

Для вертикального движения тела вблизи поверхности Земли, скорость связана с высотой законом сохранения механической энергии. Механическая энергия сохраняется, если пренебречь трением и другими потерями энергии, то есть сумма кинетической (из-за скорости) и потенциальной (из-за высоты) энергий остается постоянной.

Потенциальная энергия (P) зависит от высоты (h) и веса тела (m*g), где m - масса тела, g - ускорение свободного падения (около 9.8 м/с² на поверхности Земли):
P = m*g*h.

Кинетическая энергия (K) связана со скоростью (v) и массой (m) тела следующим образом:
K = (1/2)*m*v².

Сумма этих двух энергий должна оставаться постоянной:
P + K = m*g*h + (1/2)*m*v².

Так как нам даны графики зависимости скорости от времени для трех тел, мы можем сделать следующие наблюдения:

1) Зависимость скорости от времени для первого тела представлена синей линией. Скорость увеличивается равномерно со временем, а значит, максимальная скорость будет находиться в самом конце графика (после установления равномерного движения). Обозначим максимальную скорость первого тела как v₁.

2) Зависимость скорости от времени для второго тела представлена зеленой линией. Скорость сначала увеличивается, а затем уменьшается со временем, подобно движению вверх и вниз по параболической траектории. Максимальная скорость будет находиться в вершине параболы. Обозначим максимальную скорость второго тела как v₂.

3) Зависимость скорости от времени для третьего тела представлена красной линией. Скорость сначала уменьшается, а затем снова увеличивается со временем, подобно движению вверх и вниз по параболической траектории. Максимальная скорость будет находиться в верхней точке второго возврата. Обозначим максимальную скорость третьего тела как v₃.

Таким образом, неравенство для максимальных высот на которые поднимутся эти тела будет выглядеть следующим образом:

h₁ < h₂ < h₃,

где h₁ - максимальная высота, на которую поднимется первое тело,
h₂ - максимальная высота, на которую поднимется второе тело,
h₃ - максимальная высота, на которую поднимется третье тело.

Это неравенство объясняется тем, что максимальная высота поднятия зависит от максимальной скорости, достигаемой телом при движении вверх. Тело с большей максимальной скоростью поднимется на большую высоту.