На горизонтальной поверхности тележки лежит груз массой m1=2 кг, связанный с другим грузом массой m2=1кг с тонкой нерастяжимой нити, перекинутой через блок, укрепленный на тележке. С каким наибольшим ускорением нужно двигать тележку вправо, чтобы грузы находились в покое относительно нее? Коэффициент трения обоих грузов о поверхность тележки =0,1.
Другие вопросы по теме Физика
Популярные вопросы
- Из окна девятого этажа (h=31м) бросили камень . определите время...
1 - Транскрипция слов египет бразилия япония великобритания украина...
2 - Решить : в магазин завезли 7/18- свеклы, 112кг капусты, 30%-...
2 - Варианты предложений со словом: just?...
1 - Родственное слова заменить,обмен мина...
2 - Сочинить стих о великой отечественной войне...
2 - Из 25 учащихся в классе 8 учатся на 5 , 5- на 3 и 4 тех кто учится...
3 - Найдите все углы, образованные при пересечении двух параллельных...
1 - Расстояние между а и в 48км.из пункта а выехал велос-т со скоростью...
1 - Какой порядок действия в примере без скобок? ?...
2
Введем систему координат так: ось у (вертикальную) направим вниз, а горизонтальную ось х направим влево. Рассмотрим второй груз:
В проекции на у запишем второй з. Ньютона: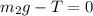 , где
, где 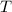 — сила натяжения нити. Такая же сила натяжения будет действовать и на первый груз (нить нерастяжима). Теперь перейдем в систему отсчета, связанную с тележкой. Формально мы можем описывать движение груза тем же вторым законом Ньютона, но придется учитывать силу инерции, равную
— сила натяжения нити. Такая же сила натяжения будет действовать и на первый груз (нить нерастяжима). Теперь перейдем в систему отсчета, связанную с тележкой. Формально мы можем описывать движение груза тем же вторым законом Ньютона, но придется учитывать силу инерции, равную 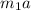 . На первый груз действует сила реакции опоры, сила натяжения нити и сила трения покоя (+сила инерции). Запишем в проекции на х:
. На первый груз действует сила реакции опоры, сила натяжения нити и сила трения покоя (+сила инерции). Запишем в проекции на х: 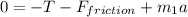 ; В нашем уравнении равновесие будет сохранятся, если правая часть неположительна. Случай "=0" соответствует максимальному значению ускорения. Найдем его:
; В нашем уравнении равновесие будет сохранятся, если правая часть неположительна. Случай "=0" соответствует максимальному значению ускорения. Найдем его: 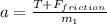 ; В этом граничном случае
; В этом граничном случае 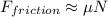 ,
, 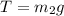 ;
;
Получаем: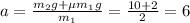 ;
;
ответ: 6 м/с^2