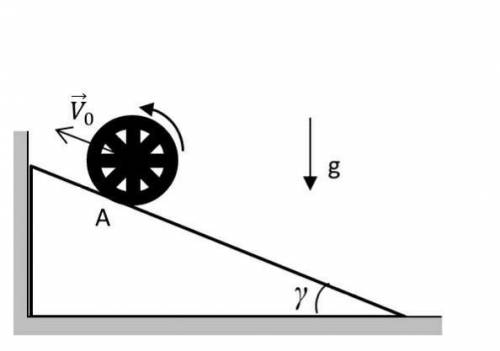
На гладкой горизонтальной поверхности стола находится призма, упирающаяся в гладкую вертикальную стенку. Поверхность призмы наклонена под углом γ к горизонту (см. рис.). Велосипедное колесо массой m движется вверх по призме, катясь без проскальзывания и имея при прохождении точки А скорость v0. При движении колеса вверх призма давит на стенку с постоянной силой F. На какое максимальное расстояние удалится колесо от точки А при движении вверх? ​

Для решения данной задачи нам потребуется применить законы динамики и закон сохранения энергии. Давайте рассмотрим их пошагово.

1. Закон динамики в направлении оси x:
На горизонтальной поверхности стола действует горизонтальная сила трения (Fтр), которая равна по модулю силе реакции опоры (N) умноженной на коэффициент трения (μ):
Fтр = N * μ.

Хотя участок движения в направлении x не указан, мы можем сказать, что движение происходит без проскальзывания, поэтому Fтр = 0.
Так как Fтр = N * μ, то так как Fтр = 0, то и N * μ = 0.
Так как μ ≠ 0 (иначе призма соскальзывала бы), то N = 0.

Таким образом, реакция опоры равна нулю, что значит, что призма не оказывает горизонтальных сил на колесо в направлении x.

2. Закон сохранения энергии:
Механическая энергия (Е) сохраняется в закрытой системе. Мы можем использовать это свойство для решения задачи.

Перед началом движения колесо имеет только кинетическую энергию (Ек) за счет его скорости. При движении вверх колесо теряет энергию из-за гравитационного потенциала (Еп).

В начальный момент времени колесо имеет кинетическую энергию Ек = (1/2) * m * v0^2 и потенциальную энергию Еп = 0.
По закону сохранения энергии:
Е = Ек + Еп = (1/2) * m * v0^2 + 0 = (1/2) * m * v0^2.

В конечный момент времени колесо имеет только потенциальную энергию Еп за счет его высоты над точкой А.
Для нахождения потенциальной энергии воспользуемся простым соотношением: Еп = m * g * h, где g - ускорение свободного падения, h - высота над точкой А.

Таким образом, в конечный момент времени:
Е = Ек + Еп = 0 + m * g * h = m * g * h.

3. Нахождение максимального расстояния:
Максимальное расстояние до точки А (d) будет достигнуто, когда будет исчерпана вся кинетическая энергия и потенциальная энергия станет максимальной.

Из предыдущего пункта мы знаем, что механическая энергия в начале равна (1/2) * m * v0^2, а в конце - m * g * h.

При движении вверх по призме кинетическая энергия колеса превращается в потенциальную энергию, а значит:
(1/2) * m * v0^2 = m * g * h.

Отсюда мы можем выразить h:
h = (1/2) * v0^2 / g.

Так как h = tg(γ) * d (по теореме Пифагора), то для нахождения d необходимо подставить h в это равенство:
tg(γ) * d = (1/2) * v0^2 / g.

Итак, ответ на вопрос: максимальное расстояние, на которое удалится колесо от точки А при движении вверх, равно:
d = (1/2) * v0^2 / (g * tg(γ)).

Надеюсь, данное объяснение поможет вам понять решение задачи. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать их!