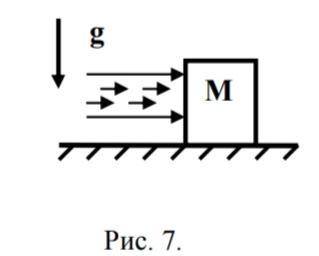
На брусок массы М направлена

струя жидкости сечения S, с плотностью ρ и

скоростью V. Найти установившуюся скорость

бруска, если коэффициент трения между бруском

и полом равен k, а взаимодействие струи с

бруском неупругое.

Добрый день!

Для решения данной задачи, нам необходимо использовать законы сохранения. Закон сохранения импульса позволяет нам решить задачу, связанную с движением бруска.

Итак, для начала, давайте определим формулу для импульса. Импульс I можно выразить как произведение массы объекта (в данном случае бруска) на его скорость:

I = M * V

Далее, по закону сохранения импульса, сумма импульсов до и после взаимодействия должна оставаться неизменной.

Таким образом, можем записать уравнение:

I до = I после

M * V до = (M + ΔM) * V после

Здесь ΔM - масса струи передачи импульса бруску. Она равна произведению плотности жидкости ρ на изменение объема струи за единицу времени ΔV:

ΔM = ρ * ΔV

Также, необходимо учитывать силу трения между бруском и полом. Сила трения Fтр можно выразить как произведение коэффициента трения k на силу нормального давления между бруском и полом P:

Fтр = k * P

Сила нормального давления равна произведению массы бруска М на ускорение свободного падения g:

P = M * g

Теперь, используя второй закон Ньютона ( Fтр = M * a), где а - ускорение бруска, можем записать:

k * M * g = M * a

Таким образом, у нас имеется система из двух уравнений:

1) M * V до = (M + ρ * ΔV) * V после
2) k * M * g = M * a

Теперь, после составления уравнений, давайте рассмотрим шаги их решения:

1) Раскрываем скобки и выражаем V после:

M * V до = M * V после + ρ * ΔV * V после

M * V до - M * V после = ρ * ΔV * V после

V после * (M + ρ * ΔV) = M * V до

V после = (M * V до) / (M + ρ * ΔV)

2) Выражаем ускорение а:

k * M * g = M * a

a = (k * M * g) / M

a = k * g

Итак, мы получили значения установившейся скорости V после и ускорения а.

Теперь, подставим значения в первое уравнение и решим задачу. Но, для этого нам необходимы численные значения массы бруска М, скорости V до, плотности жидкости ρ, коэффициента трения k и ускорения свободного падения g.

Прошу уточнить эти значения, чтобы мы могли предоставить полное решение задачи.