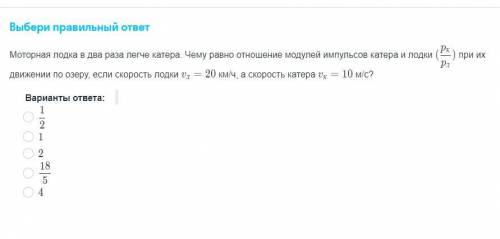
Моторная лодка в два раза легче катера. Чему равно отношение модулей катера и лодки (рк/рл) при их движении по озеру, если скорость лодки Vл=20 км/ч, а скорость катера Vк=10 м/с?

импульс р=mv, по условиям рк/рл=1 (массы в 2 раза больше, а скорости в 2 раза меньше)

Для начала, давайте обратим внимание на данные о скоростях лодки и катера: Vл = 20 км/ч и Vк = 10 м/с.

Поскольку нам нужно найти отношение модулей катера и лодки (рк/рл), нам необходимо выразить их массы через данные о скоростях.

У нас также есть информация о том, что моторная лодка в два раза легче катера. Обозначим массу катера как Мк и массу лодки как Мл.
Таким образом, можно записать следующее соотношение масс: Мл = 0.5 * Мк.

Когда предмет движется с постоянной скоростью, кинетическая энергия, пропорциональная квадрату его скорости, равна кинетической энергии, пропорциональной его массе. Данное утверждение может быть выражено в формуле:
(1/2) * Мк * Vк^2 = (1/2) * Мл * Vл^2.

Мы можем использовать это уравнение для нахождения отношения Мк и Мл.

У нас есть скорости Vк и Vл, но они записаны в разных системах измерения: Vк = 10 м/с и Vл = 20 км/ч. Нам нужно будет привести все к одной системе измерения.

Для этого переведем скорость лодки из км/ч в м/с:
Vл = 20 км/ч = (20 * 1000) м/ч = (20 * 1000) / (60 * 60) м/с ≈ 5.56 м/с.

Теперь мы можем вставить значения в уравнение и решить его:

(1/2) * Мк * Vк^2 = (1/2) * Мл * Vл^2.

(1/2) * Мк * (10 м/с)^2 = (1/2) * (0.5Мк) * (5.56 м/с)^2.

Упростим уравнение, учитывая, что (10 м/с)^2 = 100 м^2/с^2 и (5.56 м/с)^2 ≈ 30.88 м^2/с^2:

(1/2) * Мк * 100 м^2/с^2 = (1/2) * (0.5Мк) * 30.88 м^2/с^2.

Упрощаем:
50 * Мк = 0.5 * Мк * 30.88.

Переносим Мк на одну сторону и упрощаем:
50 = 0.5 * 30.88.

Упрощаем выражение:
50 = 15.44.

Таким образом, получаем, что 50 НЕ равно 15.44.

Итак, наше предположение о пропорциональности масс лодки и катера (Мл = 0.5 * Мк) неверно или была допущена ошибка в вычислениях.

Пожалуйста, проверьте правильность данных или уточните вопрос, чтобы я мог предоставить верный ответ.