Момент инерции тонкого однородного стержня относительно оси, проходящей перпендикулярно через центр масс стержня.

Ответы

ONO2017 10.10.2020 07:04

$\dfrac{ml^2}{12}$

Объяснение:

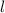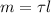Выбираем начало координат в центре масс. Линейную плотность стержня обозначим как $\tau$ , длина стержня . Тогда масса стержня $m=\tau l$ .

$\displaystyle I=\int r^2\,dm=\int_{-\frac l2}^{\frac l2}x^2\cdot\tau\,dx=\left.\tau\frac{x^3}3\right|_{-\frac l2}^{\frac l2}=\frac\tau3\cdot2\cdot\frac{l^3}8=\tau l\cdot\frac{l^2}{12}=\dfrac{ml^2}{12}$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Физика

margosha2810 09.06.2019 11:10

По двум,пересекающимся под прямым углом дорогам движутся к перекрёстку 2 автомобиля. скорость первого v,а второго 2v. какова скорость второго автомобиля относительно первого?...

gwetyalina1345 09.06.2019 11:10

Найдите разность потенциалов на пластинках конденсатора емкость 150мкф, если пластинам сообщили заряд в q=2*10^-6 кл...

anastasiykucher 09.06.2019 11:10

Определить работу электрических сил, совершенную при удалении зарядов q1=3*10^(-8) кл и q2=5*10^(-6) кл друг от друга с 20 до 50 см...

Gasdsa 09.06.2019 11:10

Через реку переправляется лодка, выдерживающая курс, перпендикулярный течению. скорость лодки 1,4 м/с скорость течения 0,70 м/с, ширина реки 308 метров. найти время, за...

дана34657 09.06.2019 11:10

Тело одновременно участвует в двух равномерных движениях, направленных под углом 120* друг к другу. скорости v1 и v2 обоих движений равны. найти величину и направление скорости...

Strelok09245 09.06.2019 11:10

Струя водяного пара при температуре 100 0с, направленная на глыбу льда, масса которой 4 кг и температура -7 0с, растопила ее и нагрела получившуюся воду до температуры 45...

ostankova82 09.06.2019 11:10

1определите длину волны де бройля для электрона, находящегося в атоме водорода на третьей боровской орбите. 2определите какую ускоряющую разность потенциалов должен пройти...

lalala106 09.06.2019 11:10

Автомобиль движется с ускорением 3м/с. какую скорость приобретёт через 5 с если его начальная скорость равна 36 км/ ч...

ledilove77 09.06.2019 11:10

Колебательный контур содержит плоский конденсатор площадью платин 250 см2, расстояние между которыми 9 мм, и катушку индуктивностью 0,25 мгн. пренебрегая активным сопротивлением...

ник4430 09.06.2019 11:10

Маятник установлен в кабине автомобиля, движущегося прямолинейно со скоростью 20 м/с. определить частоту колебаний маятника, если за время, в течение которого автомобиль...

Момент инерции тонкого однородного стержня относительно оси, проходящей перпендикулярно через центр масс стержня.

Популярные вопросы