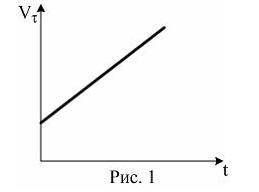
Материальная точка M движется по окружности со скоростью V⃗ . На рис. 1 показан график зависимости проекции скорости Vτ от времени (τ⃗ – единичный вектор положительного направления, Vτ – проекция V⃗ на это направление). При этом для нормального an и тангенциального at ускорения выполняются условия… Выберите один ответ:
a.
an > 0; at > 0
b.
an = 0; at = 0
c.
an > 0; at = 0
d.
an = 0; at > 0
Другие вопросы по теме Физика
Популярные вопросы
- Попалось такая с параметром, но она не простая, а с подвохом: решение a =9 по ответам...
1 - Золотая орда. что произошло в 1480 году? ...
3 - Бір фермер егіннің түсімдлігі 14ц/га ал екіншісінде 19ц/га.екі фермер де 200га...
3 - Порція галушок у кафе пампушка ...
3 - Поради к очумілому яким треба бути і яким не треба бути. (миниум 5 порад) текст...
3 - 2. переведите следующие группы существительного с конструкцией “zu + partizip i”....
2 - Перебудувати двоскладні речення на односкладні неозначено-особові. 1.у великій...
3 - сказ «левша» в сказа о левше много новых слов. словотворчество начинается там,...
2 - Скласти твір мініатюр про зимні свята з неповними і повними речення ми...
1 - Письменный ответ на вопрос: почему м.горький назвал левшу маленьким великим человеком...
3
Чтобы определить значения нормального (\( a_n \)) и тангенциального (\( a_t \)) ускорений, нам нужно анализировать изменение проекции скорости.
Нормальное ускорение (\( a_n \)) отвечает за изменение направления скорости и направлено перпендикулярно к вектору скорости в данной точке на окружности.
Тангенциальное ускорение (\( a_t \)) отвечает за изменение модуля скорости и направлено по касательной к окружности в данной точке.
На графике видно, что начальная проекция скорости \( V_{\tau} \) постоянна и равна \( V_0 \). Это означает, что скорость материальной точки постоянна и не изменяется по направлению. То есть, нормальное ускорение равно нулю (\( a_n = 0 \)).
По графику также видно, что проекция скорости (\( V_{\tau} \)) увеличивается со временем. Это указывает на то, что модуль скорости с ростом времени также увеличивается. То есть, тангенциальное ускорение \( a_t \) положительно (\( a_t > 0 \)).
Таким образом, ответ на данный вопрос будет: d. \( a_n = 0; a_t > 0 \). Нормальное ускорение равно нулю, а тангенциальное ускорение положительно.