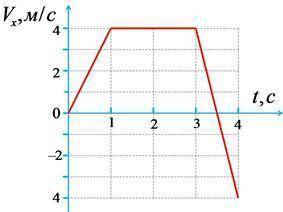
Материальная точка движется вдоль оси Ox. На рисунке показан график зависимости проекции её скорости от времени. Концы отрезков находятся точно в узлах координатной сетки. В момент начала отсчёта времени координата точки x0 = -4м. Определите координату точки в момент времени t=4 c. ответ вводите с точностью до десятых.

Хорошо, давайте разберем эту задачу пошагово.

Первое, что мы видим на графике, это изменение проекции скорости материальной точки в зависимости от времени. Если мы посмотрим на прямую, которая соединяет две точки на графике, мы можем увидеть, что это прямая линия, а значит, скорость в данном случае является постоянной.

Теперь мы должны найти координату точки в момент времени t=4 секунды. Для этого нам необходимо найти площадь под графиком от начального времени (t=0) до нужного времени (t=4), и затем прибавить ее к начальной координате.

Для нахождения площади под графиком используем формулу S = V * t, где S - площадь, V - скорость, t - время.

Мы можем разделить путь на два отрезка: первый от t=0 до t=2 секунды и второй от t=2 до t=4 секунды. Так как скорость является постоянной, мы можем найти площадь каждого отрезка, используя формулу S = V * t.

Для первого отрезка имеем:
V1 = 2 м/c, t1 = 2 секунды.
S1 = V1 * t1 = 2 * 2 = 4 м.

Для второго отрезка имеем:
V2 = -1 м/c, t2 = 2 секунды.
S2 = V2 * t2 = -1 * 2 = -2 м.

Теперь мы можем найти общую площадь под графиком:
S_total = S1 + S2 = 4 - 2 = 2 м.

Поскольку начальная координата материальной точки x0 = -4м, мы должны добавить эту площадь к начальной координате, чтобы найти координату точки в момент времени t=4 секунды:
x = x0 + S_total = -4 + 2 = -2 м.

Таким образом, координата точки в момент времени t=4 секунды составляет -2 метра.