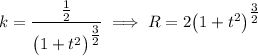Материальная точка движется по закону x = 2t, y = t². Выразите зависимость радиуса кривизны траектории от времени
Другие вопросы по теме Физика
Популярные вопросы
- Метилпропанат, составить по названию, напишите реакцию получения...
3 - Найдите сумму квадратов корней уравнения: 2x^2+5x-3=0 решите...
3 - Українські землі, що перебували у складі великого князівства литовського...
2 - Вопрос жизни и смерти. √3x+1-√x-1=2...
3 - Вкаком варианте ответа выделенное слово употреблено неверно? 1) её звучный...
2 - Сколько тысяч составляет 8 десятков тысяч?...
2 - Напишите 10 тезисов на тему политическая культура...
3 - Put on - надевать а как сказать я надел так и будет put on ? как тогда...
3 - Радиус основания конуса равен 7 см, высота 12 см найти полную поверхность...
1 - Укажите пример с ошибкой в образовании формы слова 1) ни разу не 2)менее...
3
При движении по кривой ускорение материальной точки складывается из нормальной составляющей и тангенциальной (причем они ортогональны):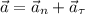
Найдём модули всех указанных векторов.
1)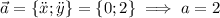
2)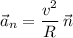 , где
, где 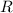 - радиус кривизны в данной точке (момент времени). Причём,
- радиус кривизны в данной точке (момент времени). Причём, 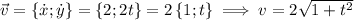 . Таким образом,
. Таким образом, 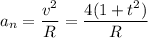
3)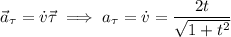
Поскольку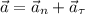 и
и 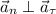 , то из прямоугольного треугольника на трёх указанных векторах получим:
, то из прямоугольного треугольника на трёх указанных векторах получим:
ответ.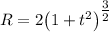
PS. Наиболее быстро ответ можно получить с дифференциальной геометрии.
Кривизной траектории выраженной явно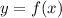 называется величина
называется величина 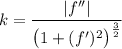 , а радиусом кривизны - величина
, а радиусом кривизны - величина 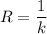 .
.
Для нашей задачи,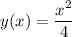 . Отсюда
. Отсюда 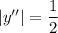 и
и 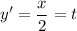 .
.
Сразу же получаем