Математический маятник имеет длину 38 м Определите период и частоту колебаний такого маятника. ПРИ расчётах прими 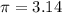
Другие вопросы по теме Физика
Популярные вопросы
- Вроде лёгкая задача, но совсем не шарю.....
2 - Осередки напруження у міжнародних відносинах у 20-х - на поч. 30-х років:...
3 - 1) Определите число атомов, молекул, электронов в: 17 г монофторметана;...
3 - ABCA1B1C1 – правильная треугольная призма со стороной основания AB=12 и...
2 - Определите коэффициент и степень одночлены 7а⁶в²/8а3 если что черта это...
1 - Плотность водного раствора соляной кислоты HCl (ω(HCl) =36.2%) равна 1.18...
1 - Сочинение – миниатюра « Мой любимый герой »....
3 - Які історичні події відбувались на землі пиктів балада вересовий трунок...
2 - сумма вертикальных углов мое и дос, образованных при пересечении прямых...
2 - Считайте это халявные Упростите выражение:...
2
Математический маятник - это система, состоящая из точки крепления и материальной точки, которая свободно вращается вокруг точки крепления. Чтобы найти период и частоту колебаний математического маятника, мы будем использовать формулы, связывающие длину маятника и период колебаний.
Период колебаний (T) - это время, за которое маятник совершает одно полное колебание (возвращается в исходное положение). Он измеряется в секундах.
Частота колебаний (f) - это количество полных колебаний, совершаемых маятником в единицу времени. Она измеряется в герцах (1 Гц = 1 колебание в секунду).
Формула для расчета периода колебаний математического маятника:
T = 2π√(L/g)
где L - длина маятника (в метрах), g - ускорение свободного падения (приближенное значение g = 9,8 м/с²).
Давайте подставим значения, чтобы найти период:
T = 2π√(38/9.8)
T = 2π√(3.877)
T ≈ 2π * 1.969
T ≈ 12.388 сек
Таким образом, период колебаний математического маятника с длиной 38 м составляет около 12.388 секунд.
Теперь давайте найдем частоту колебаний:
f = 1/T
f ≈ 1/12.388
f ≈ 0.0807 Гц
Таким образом, частота колебаний математического маятника с длиной 38 м составляет около 0.0807 Гц.
Такое детальное объяснение помогает понять школьнику, почему мы используем определенные формулы и как мы приходим к окончательному ответу.